- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
More Than Just a Grade: The HOM SIGMAA Student Contest Fosters Writing Excellence at UMKC - Sample Explication
I think it wise to provide examples to my students of what sort of explication product I expect. As I explain, I don’t require them to produce as complete a document as mine, but in reading my sample they should see what is possible with a little care and enough time on task. Every document requires multiple passes and close reading at both the level of fine detail and the level of structure and argumentation to reveal what explication is needed. A cursory glance (meaning just one quick draft) will inevitably miss important features, as I have found to my chagrin often enough in my own work. Here’s one of my samples. The original author’s document can be found here: Fibonacci On Two Birds Source (pdf). A second example document and my corresponding explication can be found in the following two documents: Alkhwarizmi Quadratic Equation Source (pdf) and Alkhwarizmi Quadratic Equation Explication (pdf).
One Explication SAMPLE provided to students
Math 464 WI History of Mathematics R. Delaware
A Transcription and Explication using Modern English and Notation
From: Leonardo Pisano (Fibonacci), c.1170–c.1240, born in Pisa, in (what is now) Italy, from Liber Abaci (Book of Calculation), 1202, Chapter 13, Part One, as translated by L. E. Sigler in Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, New York: Springer, 2002, pp. 462–463.
Notes: All comments in [square brackets] and illustrations are mine.
On Two Birds
Two birds were above the height of two towers; one tower was 40 paces in height and the other 30, and they [the towers] were 50 paces apart; at an instant the pair of birds descended [from the tops of the towers] flying to the center [some point between the towers, not necessarily the exact center] where there was a fountain, and they arrived at the same moment at the fountain which was between both towers. From the moment they left until the moment they arrived they flew in straight lines from the tops of the towers to the center of the fountain; the flights were of equal lengths [distances];

[The unstated question is: Where is the center of the fountain located? Now, we start on a solution.]
in geometry it is clearly demonstrated that the height of either tower multiplied by itself added to the distance from the tower to the center of the fountain multiplied by itself is the same as the straight line from the center of the fountain to the top of the tower multiplied by itself [This is a statement of the Pythagorean Theorem, Euclid I.47.];
this therefore known, you put it that the distance from the center of the fountain to the higher tower is any number of paces, we say 10,
[a first “false position” guess. Here he begins an application of the so-called “Method of Double False Position” (which my students have already studied; see the Note following this explication). We’ll discuss below whether this is appropriate.]
and you multiply the 10 by itself; there will be 100 that you add to the height of the higher tower multiplied by itself, namely to 1600; there will be 1700 that you keep [the result of his first application of the Pythagorean Theorem to the “higher tower” right triangle], and you multiply by itself the remaining distance, namely the 40 which is the distance from the center [of the fountain] to the lower tower; there will be 1600 which you add to the height of the lower tower multiplied by itself, namely 900; this makes 2500 [the result of his second application of the Pythagorean Theorem to the “lower tower” right triangle] that should be 1700 [because the bird flights (hypotenuses) were of “equal lengths”] as was the sum of the other two products; therefore [the value of] this position is long of the true value by 800, namely the difference between 1700 and 2500
[The value of “this position” is really the difference “lower tower sum of squares – higher tower sum of squares”, a function of the “position”, which here is 10 paces. But, since the bird flights (each a hypotenuse) were of “equal lengths”, the squares of those lengths are then also equal, so by the Pythagorean Theorem the “true value” of “lower tower sum of squares – higher tower sum of squares” must therefore be zero!];
therefore you lengthen the distance from the center of the fountain to the higher tower; indeed it is lengthened 5 paces from the first position, namely 15 paces [the second “false position” guess] from the center [of the fountain] to the higher tower, and you multiply the 15 by itself; there will be 225 which you add to height of the higher tower multiplied by itself, namely 1600; there will be 1825. Similarly you multiply by itself the 35 which is the distance from the center of the fountain to the lower tower making 1225 [corrected from typographic error “12225”]; this added to the 900, namely the height of the higher [should be “lower”] tower multiplied by itself, makes 2125 that should be 1825 by the abovewritten [sic] rule [again, because the bird flights (hypotenuses) were of “equal lengths”]. Therefore the value of the second position is an amount long of the true value by 300
[Once again, the “value of the second position” is really “lower tower sum of squares – higher tower sum of squares”, a function of the “second position”, here 15 paces. So, the “true value” is again zero.];
the first value was long indeed by 800; therefore you say:
for the five paces which we lengthened the distance from the center of the fountain to the higher tower we approximated more closely to the true value by 500 [800 – 300 = 500]; how much indeed shall we lengthen the distance from the center of the fountain to the same higher tower in order to improve the approximation by [an additional] 300?
You multiply the 5 by the 300, and you divide by 500; the quotient will be 3 paces [written within a small “answer” box below]

[The idea is that when \(\frac{5}{500}=\frac{\Delta}{300}\), it follows that \(\frac{5\cdot300}{500}= \Delta=3\). The large box above is meant to suggest, reading horizontally, that since a change of 500 was caused by an increase of 5 paces, then a change of 300 will be caused by an increase of 3 paces. The two *s on the main diagonal indicate the multiplication of “5 by the 300”.]
which added to the 15 paces yields 18 paces, and this will be the distance from the [center of the] fountain to the higher tower. Truly the remaining distance, namely the 32 [which is 50 – 18], is the distance to the lower tower.
[Finally, he checks the solution.]
For example, the product of the 18 by itself added to the product of the 40 by itself makes as much as the product of the 32 by itself added to the product of the 30 by itself, as had to be. [182 + 402 = 322 + 302 (= 1924).]
A Modern Direct Solution
Let \(x\) = the distance from the higher tower to the center of the fountain, so that
\(50 - x\) = the distance from the lower tower to the center of the fountain.
By the Pythagorean Theorem, since the bird flight lengths (each a hypotenuse) are equal, and hence the squares of those lengths are equal, the problem requires that
[Higher tower sum of squares] = [Lower tower sum of squares]:
\[\begin{array}{ccc} x^2 + 40^2 &=& (50-x)^2+30^2\\x^2 + 40^2 &=& 50^2 - 100x +x^2+30^2 \\ 100x + 40^2 -50^2 -30^2 &=&0 \\100x - 2\cdot 30^2 &=&0\\100(x-18)&=&0\\x&=&18\end{array} \]
So \(x= 18\) paces is the solution. Notice that it becomes clear at the third equation that in fact this is a linear equation (the “squared” powers add to zero) of the form \(ax = b\), justifying the use of the Method of Double False Position, which only applies to such linear relationships (functions).
Note: The Method of Double False Position
(called by Leonardo Pisano “elchataym”, an Arabic word)
[Based on comments by the translator L. E. Sigler of Leonardo Pisano’s Liber Abaci (Book of Calculation), 1202, translation published 2002, p. 628.]
Using modern notation, the idea is that to solve a linear equation \(ax+b=c\) for \(x\), pick two arbitrary values for \(x\), say \(x_1\) and \(x_2\) each of which is unlikely to be the correct value for \(x\), hence are in general called “false position” values. Substitute them into \(ax+b=c\) to obtain \(ax_1+b=c_1\) and \(ax_2+b=c_2\). From these two equations solve for both \(a\) and \(b\), then substitute those results back into \(ax+b=c\) , and finally solve for \(x\) to get:
\[ x=x_2+\frac{(c_1-c_2)(x_2-x_1)}{c_2-c_1}.\]
In “On Two Birds,” \(x_1 = 10\), \(x_2=15\), \(c_1=800\), \(c_2=300\), and \(c=0\), the “true value,” yielding the quotient
\[\Delta = \frac{(c_1-c_2)(x_2-x_1)}{c_2-c_1} = \frac{(0-300)(15-10)}{300-800}=\frac{-300(5)}{-500} = 3 ,\]
so that \(x = 15+3 = 18\), as desired. Also, in this modern notation, the proportion visualized in the “On Two Birds” box
\( \displaystyle{\frac{5}{300} = \frac{\Delta}{300}} \) is \( \displaystyle{\frac{x_2-x_1}{c_1-c_2} = \frac{\Delta}{c_2-c_1}} \)
matching exactly the calculation of \(\Delta\) above (and avoiding the appearance of any negative numbers, which Leonardo would not have used).
A Modern Interpretation of the Leonardo Pisano Solution
Using \(x\) and \( 50 – x\) as above, he examines the function of \(x\) (“the value of the position”) given by
\[ f(x) = \mbox{ [Lower tower sum of squares] -[Higher tower sum of squares]} \] meaning \[ f(x) = \left [ (50-x)^2 + 30^2 \right ] - \left [ x^2 + 40^2\right ] \]
which he desires to equal zero (the “true value”), that is, \(f(x) = 0\).
Using the Method of Double False Position (which does apply here since the function is actually linear), he first calculates
\( f(10) = 800 \) then \( f(10 + 5) = 300 = 800 – 500 \) ,
determining the points (10, 800) and (15, 300) lying on the desired line, and he finds the solution by extending that line until it meets the horizontal axis. That is, he concludes that if an increase (from 10 paces) of \(x\) by 5 paces yields a decrease of \( f(x) \) by 500, then a further increase of \(x\) by 3 paces will yield an additional decrease of \( f(x) \) by 300, meaning a decrease to zero. Thus \( x = 15 + 3 = 18\) paces is the solution.
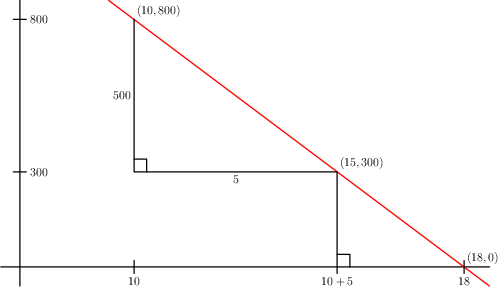
By the way, the equation of that line is \( y = 1800 - 100 x = 100 (18-x) \).
Richard Delaware (University of Missouri - Kansas City), "More Than Just a Grade: The HOM SIGMAA Student Contest Fosters Writing Excellence at UMKC - Sample Explication," Convergence (February 2019)




