- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
On Squares, Rectangles, and Square Roots - Results
 |
 |
|
Operations performed by a student to calculate \(\sqrt{196}\). |
Graphical representation of completing the square to get \(\sqrt{196}\). |
Figure 5. Details of a student's graphical calculation of \(\sqrt{196}\).
As described in the preceding section, students were to implement a method from ancient China for computing the following square roots of three-digit integers:
(a) \(\sqrt{196},\) (b) \(\sqrt{484},\) (c) \(\sqrt{256},\) and (d) \(\sqrt{576}.\)
The students were to:
- use manipulatives (squares and rectangles) to construct a square with side length equal to the square root,
- transcribe the operations used for the decomposition, and
- draw the geometric construction on a grid with numbered axes.
Figures 5-7 on this page show samples of students' written work. Figures 4a and 4b on the preceding page show students' constructions with manipulatives. Table 1 summarizes students' performance.
Table 1. Absolute and relative (%) frequencies of students' resolutions (\(n\)=69):
| Items | ||||
| Categories | \(\sqrt{196}\) | \(\sqrt{484}\) | \(\sqrt{256}\) | \(\sqrt{576}\) |
|
Root result is not expressed Root result is expressed, but it is wrong Root result is expressed and is correct |
8 (11.59) 0 (0) 61 (88.41) |
5 (7.24) 0 (0) 64 (92.76) |
11 (15.94) 0 (0) 58 (84.06) |
8 (11.59) 1 (1.45) 60 (86.96) |
|
Decomposition is not accomplished Decomposition is incorrectly accomplished Decomposition is correctly accomplished |
6 (8.70) 17 (24.64) 46 (66.66) |
6 (8.70) 17 (24.64) 46 (66.66) |
10 (14.49) 14 (20.28) 45 (65.22) |
7 (10.14) 21 (30.44) 41 (59.42) |
|
Graphic representation is not done Graphic representation is done, but not properly Graphic representation is properly done |
2 (2.90) 0 (0) 67 (97.10) |
1 (1.45) 3 (4.35) 65 (94.20) |
4 (5.80) 5 (7.24) 60 (86.96) |
1 (1.45) 5 (7.24) 63 (91.30) |
Table 1 shows that, on average over the four examples, more than 92% of the students adequately drew the geometric representation of the construction using the Kai Fang method. However, around 35% of the students had difficulties adequately expressing the decomposition of the radicand as the sum of the areas of the figures used in the construction, item (d) being the one that gave them the greatest difficulty in this sense. For item (d), 40.58% of children did not perform well the decomposition of 576. This may be due to the fact that some students tried to decompose the radicands by means of only their hundreds, tens and units without considering the geometric distribution. Thus, while in sections (a) \(\sqrt{196}\) and (b) \(\sqrt{484}\) the figures of the hundreds, 1 and 4 (100 and 400), corresponded to perfect squares, the same did not happen with (c) \(\sqrt{256}\) and (d) \(\sqrt{576}\), for which 2 and 5 (200 and 500) required “completion”.
More specifically, students should have decomposed the numbers (a) \(196,\) (b) \(484,\) (c) \(256,\) and (d) \(576\) as follows:
|
(a) \(196\) \(\phantom{x}\) \(\phantom{x}\) \(\phantom{x}\) |
\(=100+90+6\) \(=100+80+10+6\) \(=100+40+40+16\) \(=10\cdot10+4\cdot10+4\cdot10+4\cdot4.\) |
|
(b) \(484\) \(\phantom{x}\) \(\phantom{x}\) |
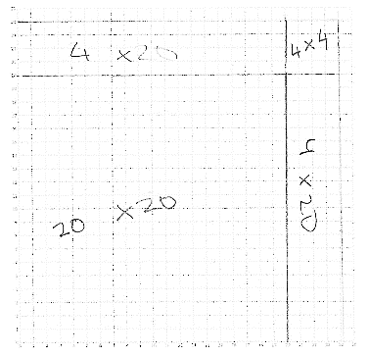
\(=400+80+4\) \(=400+40+40+4\) \(=20\cdot20+2\cdot20+2\cdot20+2\cdot2.\) |
|
(c) \(256\) \(\phantom{x}\) \(\phantom{x}\) \(\phantom{x}\) \(\phantom{x}\) |
\(=200+50+6\) \(=100+150+6\) \(=100+120+36\) \(=100+60+60+36\) \(=10\cdot10+6\cdot10+6\cdot10+6\cdot6.\) |
|
(d) \(576\) \(\phantom{x}\) \(\phantom{x}\) \(\phantom{x}\) |
\(=500+70+6=400+170+6\) \(=400+160+40+16\) \(=400+80+80+40+16\) \(=20\cdot20+4\cdot20+4\cdot20+4\cdot4.\) |
Figures 6 and 7 show student work on the trickier tasks (c) \(\sqrt{256}\) and (d) \(\sqrt{576}\):
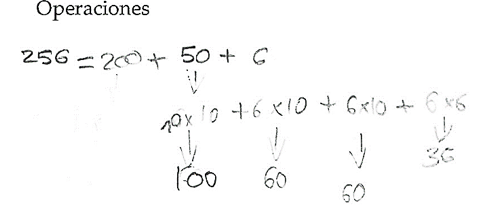 |
 |
|
Operations made by a student to get \(\sqrt{256}\). |
A graphic representation of the completing of the square to get \(\sqrt{256}\). |
Figure 6. Details of Kai Fang calculation for \(\sqrt{256}\).
 |
 |
|
Operations performed by a student to calculate \(\sqrt{576}\). |
Graphical representation of completing the square in\(\sqrt{576}\). |
Figure 7. Details of Kai Fang calculation of \(\sqrt{576}\).
As reported in Table 1, more than 84% of the students wrote correctly the result for all four of the requested roots. For most of the students who did not express the result of the calculation of the roots, the associated graphical representations were correct and we suspect a lapse in transcription. All 8 of those who did not write the result of \(\sqrt{196}\) performed the graphical representation correctly, and 3 of the 5 who did not write the result of \(\sqrt{484}\) did correctly decompose 484. Four of the 11 students who did not itemize the result for \(\sqrt{256}\) had properly performed the decomposition but made errors in the graphic representation. Finally, only 3 of the 8 students who did not write the result for \(\sqrt{576}\) did the graphic representation wrong.
Therefore, we can conclude that the types of errors detected are the following:
- When students express the result, they identify the decomposition of the radicand with the root, or they do not recognize the radical symbol and write that the root of the number is equal to the number itself.
- Arithmetic or expression errors; equalities are interwoven in the operations carried out to decompose the area.
- The decomposition does not correspond to the sum of the areas of the squares and rectangles.
- The student does not complete the square well.
These errors will be illustrated in the next section of this article.
María Burgos (University of Granada, Spain) and Pablo Beltrán-Pellicer (University of Zaragoza, Spain), "On Squares, Rectangles, and Square Roots - Results," Convergence (December 2018)




