- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Pythagorean Cuts – Rectangles and Other Parallelograms
In Figure 3, below, right triangle ABC with right angle at B is given with side lengths \(a, b,\) and \(c\) as shown. Rectangles are constructed on each side so that the width of the rectangles is the side length multiplied by some positive constant \(k,\) \(k\not=1\) (in Figure 3, \(k\) is about \(0.4\)). Can rectangle AJHC be divided up, or partitioned, in a natural way to illustrate the equation \[ka^2 + kb^2 = kc^2\] geometrically? In particular, can we proceed much as Euclid did for squares?
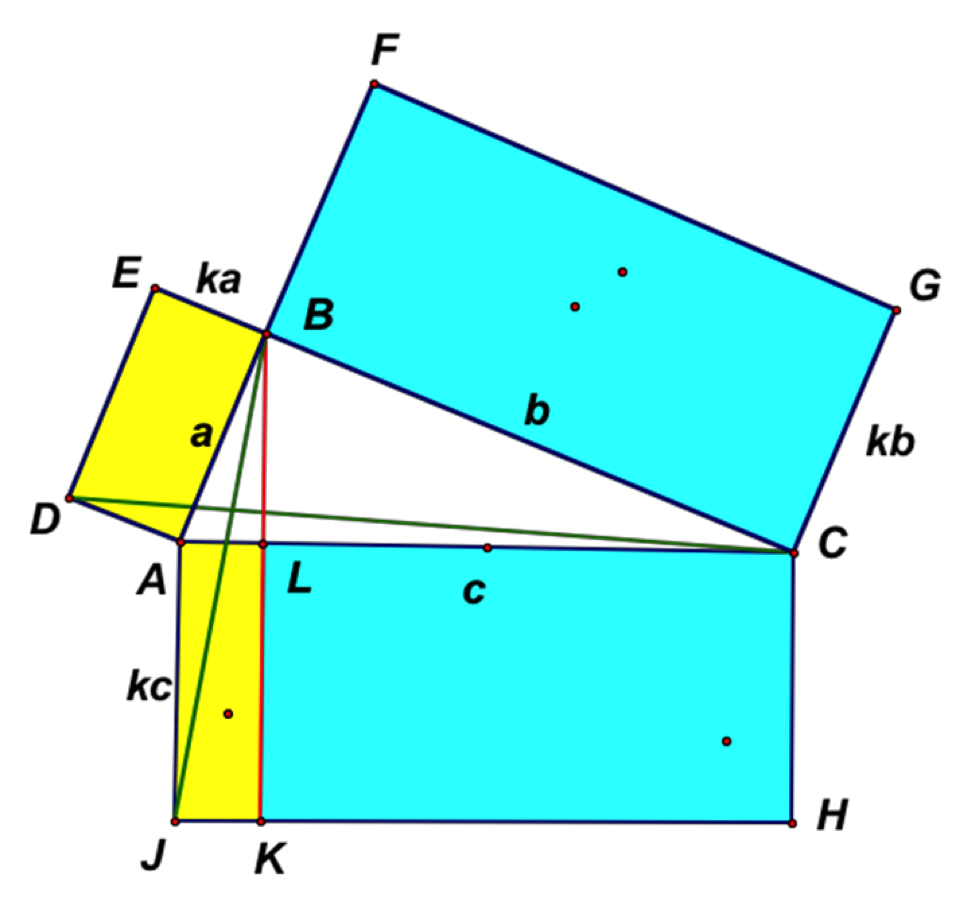
Figure 3: Similar rectangles on the sides of a right triangle. The Pythagorean cut, LK, is shown in red.
Following Euclid's proof of the Pythagorean Theorem, let BK be perpendicular to JH at K and intersect AC at L; draw construction lines DC and BJ, shown in green in Figure 3, above. We notice two things right away, one the same and one different from the situation in I.47 in which squares are drawn on the three sides. First, since triangle DAC and rectangle DABE share the same base DA and are in the same parallels with altitude AB, the area of rectangle DABE is twice the area of triangle DAC. Similarly, the area of rectangle AJKL is twice the area of triangle JAB. And second, although triangles DAC and JAB have a pair of congruent angles (JAB and DAC), the triangles are not congruent, since DA = JA only if \(a = c,\) which is impossible since \(c\) is the length of the hypotenuse, and AJ = AC only if \(k =1,\) which was not an option.
Even though triangle DAC is not congruent to triangle JAB, how do their areas compare? Triangle DAC, with base DA \(= ka\) and altitude AB \(= a,\) has area \({\frac{1}{2}}ka^2.\) Since the right triangles ALB and ABC are similar, we have \({\frac{AL}{a}}={\frac{a}{c}}.\) Hence, \(c\,AL = a^2,\) so that the area of triangle JAB is
\[{\frac{1}{2}}kc\,AL ={\frac{1}{2}}ka^2.\]
Thus, even though the two triangles are not congruent,
Area of triangle DAC = Area of triangle JAB,
so that
Area of rectangle DABE = Area of rectangle AJKL.
Similarly, we have
Area of rectangle BCGF = Area of rectangle KHCL,
so that
Area of rectangle ACHJ = Area of rectangle BCGF + area of rectangle DABE.
As in Euclid I.47, if point L is the foot of the perpendicular from B to AC, segment LK, perpendicular to hypotenuse AC (and parallel to rectangle side AJ), gives the natural partition of rectangle ACHJ. Thus, LK, shown in red in Figure 3, above, is the Pythagorean cut of rectangle ACHJ. A GeoGebra applet showing the Pythagorean cut for similar rectangles is given in Figure 4, below.
Figure 4: Pythagorean cut for similar rectangles
Please note that if similar parallelograms, rather than similar rectangles, were constructed on the sides of right triangle ABC, with point L determined as before and LK again the segment parallel to side AJ (see Figure 5, below), then the Pythagorean relationship among the areas of these parallelograms is still valid. That is,
Area of parallelogram AJKL = Area of parallelogram EDAB
and
Area of parallelogram LKHC = Area of parallelogram BCGF,
so that
Area of parallelogram EDAB + area of parallelogram BCGF = Area of parallelogram AJHC.
Again, LK is the Pythagorean cut for parallelogram ACHJ.

Figure 5: Similar parallelograms on the sides of a right triangle. The Pythagorean cut, LK, is shown in red.
Martin Bonsangue (California State University, Fullerton) and Harris Shultz (California State University, Fullerton), "Pythagorean Cuts – Rectangles and Other Parallelograms," Convergence (December 2015)




