- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Pythagorean Cuts – Triangles
Let similar right triangles ABE, BCG, and CAJ be constructed on the three sides of right triangle ABC with EB \(= ka,\) CG \(= kb,\) and AJ \(= kc,\) for some positive constant \(k,\) as shown in Figure 6, below.

Figure 6: Similar right triangles on the sides of a right triangle. Line segment LJ is the Pythagorean cut.
Although our result will follow directly from the case of rectangles (and I.41), our goal here is to determine the Pythagorean cut. As before, let L be the foot of the perpendicular from B to AC and draw LJ. Let rectangles ABED, BCGF, and CAJH be formed on right triangles ABE, BCG, and CAJ, respectively. Since we know that the area of rectangle ABED equals the area of rectangle AJKL, half of these areas are still equal to one another. Thus,
area of triangle ABE = area of triangle ALJ,
and similarly,
area of triangle BCG = area of triangle CJL.
Then
area of triangle ABE + area of triangle BCG = area of triangle AJC
and segment LJ is the Pythagorean cut for right triangle AJC.
Suppose now that any three similar triangles are constructed on the sides of right triangle ABC with triangle AE'B on side AB; triangle BG'C on side BC; and triangle CJ'A on side AC (see Figure 7, below).
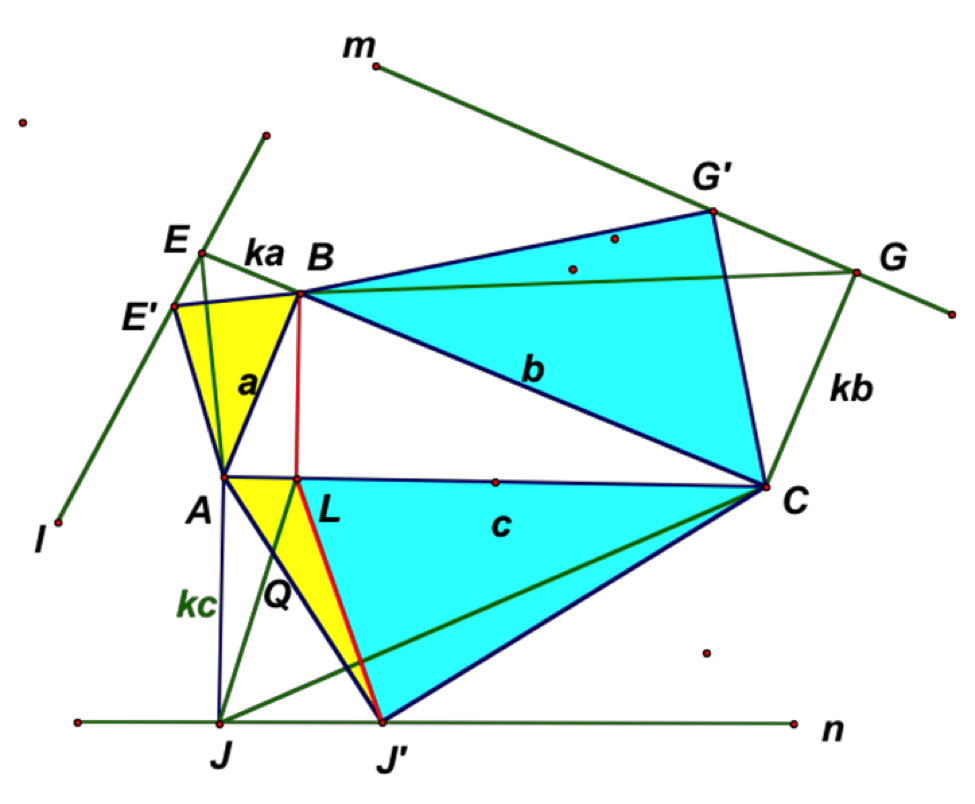
Figure 7: Similar triangles on the sides of a right triangle. Line segment LJ' is the Pythagorean cut.
Similar to the case for constructing right triangles, the result will follow from the preceding result and I.37, but finding the Pythagorean cut requires a bit more care. Let lines l, m, and n be parallel to sides AB, BC, and AC, respectively, as shown, and let segment LJ' be drawn. From Euclid I.37, we know that triangles with the same base and in the same parallels (with equal altitudes) are equal in area. Thus,
Area of triangle AE'B = Area of triangle AEB;
Area of triangle BG'C = Area of triangle BGC;
and
Area of triangle CJ'A = Area of triangle CJA.
Since triangles ALJ and ALJ' have the same base (AL) and are in the same parallels (with altitude AJ),
Area of triangle ALJ = Area of triangle ALJ'.
Since we know that
Area of triangle AEB = Area of triangle ALJ,
we have
Area of triangle AE'B = Area of triangle ALJ'.
Similarly,
Area of triangle BG'C = Area of triangle CJ'L.
Thus,
Area of triangle ABE' + Area of triangle BCG' = Area of triangle ACJ',
and segment LJ' is the Pythagorean cut for triangle AJ'C.
Martin Bonsangue (California State University, Fullerton) and Harris Shultz (California State University, Fullerton), "Pythagorean Cuts – Triangles," Convergence (December 2015)




