- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Archimedes (287-212 BCE), Greece-Italy
The Greek mathematician, scientist, and inventor Archimedes spent most of his life in Syracuse in southern Italy. Considered the greatest mathematician of antiquity, he is famous for a number of mathematical and scientific discoveries and also for a number of inventions, many of them machines of war used in his city’s defense against Roman armies. Archimedes knew the Pythagorean “formula” for the sum of the first n positive integers. He almost certainly knew also a “formula” for the sum of the squares of the first n positive integers. His Lemma to Proposition 2 in On Conoids and Spheroids (Heath, p. 57) and his Proposition 10 in On Spirals (Heath, pp. 68-69), translated to our symbols, say that
$$(n + 1)n^2 + (1 + 2 + 3 + \cdots + n) = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 )\quad (*),$$
as illustrated in Figure 3 (see also Nelsen, p. 77, and Stein, pp. 46-49).
Figure 3 shows literally that
$$3(1^2 + 2^2 + 3^2 + 4^2 ) = 5 \cdot 4^2 + (1 + 2 + 3 + 4).$$
Using the Pythagorean formula to replace \(1 + 2 + 3 + · · · + n\) by \({{n(n + 1)} \over 2}\) in Archimedes' equation
$$(n + 1)n^2 + (1 + 2 + 3 + \cdots + n) = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 )\quad (*),$$
we have
$$(n + 1)n^2 + {\frac{n(n + 1)}{2}} = 3(1^2 + 2^2 + 3^2 + \cdots + n^2 ).$$
Solving for the sum of squares, we get
$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {\frac{(n + 1)n^2}{3}} + {\frac{n(n + 1)}{6}},$$
or $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}$$
for all positive integers n.
Since Archimedes concluded in a Corollary to his Lemma to Proposition 2 (Heath, p. 57) that
$$3(1^2 + 2^2 + 3^2 + \cdots + n^2 ) > n^3 > 3(1^2 + 2^2 + 3^2 + \cdots + (n - 1)^2 ),$$
presumably, he, too, replaced \(1 + 2 + 3 + · · · + n\) by \({{n(n + 1)} \over 2}\) in his equation (*), and deduced that
$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}.$$
Again, Archimedes would have described these equations and inequalities in words rather than symbols.
Exercise 2: Use cubes (or squares) to represent the triangular numbers and to illustrate the identity
$$1 + 2 + 3 + \cdots + n = {{n(n + 1)} \over 2}$$
and the identity from Exercise 1.
Exercise 3: Use 60 or 120 cubes to illustrate the identity
$$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}$$
for n = 3 or n = 4. Hint: One way to construct a pyramid representing the sum of the first four triangular numbers, 1, 3, 6, and 10, is to place a single cube representing 1 atop a configuration of three cubes, which, in turn, is placed atop a configuration of 6 cubes, as shown in Figure 4. Just one more layer of 10 cubes will result in a pyramid containing 1 + 3 + 6 + 10 cubes. How many such pyramids should you construct in order to form a 4-cube by 5-cube by 6-cube rectangular solid? (Nelsen, p. 95)
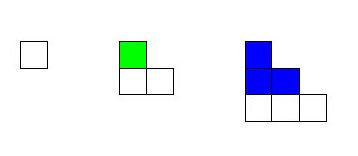
Figure 4. Place the single cube atop the shaded portion of the layer of three cubes. Place the resulting pyramid of 1 + 3 cubes atop the shaded portion of the layer of six cubes. Only tops of cubes are shown.
Solutions to these exercises can be found here.
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Archimedes (287-212 BCE), Greece-Italy," Convergence (July 2010), DOI:10.4169/loci003284




