- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Pythagoras (c. 570-500 BCE), Turkey-Greece-Italy
The Greek mathematician, philosopher, and mystic Pythagoras is said to have lived with his followers, the Pythagoreans, at Croton in what is now southern Italy. The Pythagoreans took as their motto “All is Number” and were believed to have experimented with number properties by arranging pebbles on a flat surface. As a result, they saw what we would describe as a sum of successive positive integers as a triangle or triangular number (Fig. 1).
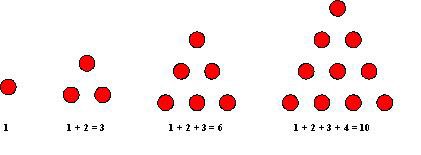
Figure 1. The first four triangular numbers
Their pebble experiments led them to see that two copies of the same triangular number could be fitted together to form an oblong number; hence, for example, twice the triangular number 15 = 1 + 2 + 3 + 4 + 5 could be viewed as the oblong number 5 x 6 = 30 (Fig. 2).
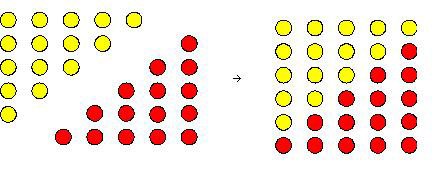
Figure 2. Twice a triangular number is an oblong number, or, in modern notation, \(2(1 + 2 + 3 + \cdots + n) = n(n + 1).\) Here we see that \(2(1 + 2 + 3 + 4 + 5) = 5\cdot 6.\)
Equivalently, any triangular number was half an oblong number; for example,
$$1 + 2 + 3 + 4 + 5 = {{5 \cdot 6} \over 2},$$
and, in general,
$$1 + 2 + 3 + \cdots + n = {{n(n + 1)} \over 2}$$
for any positive integer n.
Exercise 1: Use pebbles to illustrate that the sum of every two consecutive triangular numbers is a square number. Hint: Examples of pairs of consecutive triangular numbers include 6 and 10, 10 and 15, and 15 and 21.
The solution to this exercise is available here.
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Pythagoras (c. 570-500 BCE), Turkey-Greece-Italy," Convergence (July 2010), DOI:10.4169/loci003284




