- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Educational Times Database: Indexing MQ and ET’s Mathematical Problems, 1940s–2000s
The development of the ET database project encompasses the interlinked work of many individuals over many decades. The relevant germinal work dates to the 1940s and 1950s, when Dr. Raymond Clare Archibald (1875–1955) at Brown University, Rhode Island, led an effort to index the full run of questions and solutions published in MQ, from its first issue in 1864 to its last in 1918. Archibald’s project aimed at a specific kind of indexing, in which the “contents of a serial publication,” such as a newspaper or magazine, are cited in a list by reference to author and/or subject [Reitz 2020]. Archibald was predisposed to initiate such a project, since his twin interests were in mathematics and librarianship.

Figure 10. Portraits of Dr. Raymond Clare Archibald, a librarian and professor of mathematics
at Brown University from 1908 to 1955 [“Archibald” 2020; MacTutor].
Originally from Nova Scotia, Canada, Archibald graduated from Harvard University in 1895, completed his doctorate in mathematics at the University of Strasbourg in France at the turn of the century, and then worked several years as a college librarian in Canada [MacTutor]. In that capacity, he oversaw the acquisition of thousands of books, and he hand-wrote tens of thousands of library catalog cards. In 1908 he earned a position as instructor of mathematics at Brown University, working his way up to full professor by 1923, before retiring to an emeritus role after 1943. Sometime during his emeritus years, if not before, Archibald began indexing MQ content with the help of his students. His interest derived principally, it seems, from the fact that he had been a major contributor to the journal in his younger years [Tattersall and McMurran 2004]. Also, as a keen book collector who “frequently … went to Europe for the summer” to acquire mathematics books, journals, and dissertations for Brown University’s library, Archibald would have been aware of the historical significance of the ET for the Anglo-American mathematics community [MacTutor].
Archibald’s indexing project was left uncompleted upon his death in 1955, and it might have remained so if, decades later, another mathematician had not discovered the preserved remains of the project on the shelves of the Brown University Science Library. Dr. James Tattersall, Jr., a professor and historian of mathematics at Providence College, Rhode Island, spent considerable time in Brown’s Science Library as his own career was taking off in the late 1960s and early 1970s [Tattersall 2020]. During one of his library sojourns, Tattersall discovered five small boxes shelved next to a full set of MQs. In the boxes he found hundreds of handwritten file cards penned by Archibald and his students: the beginnings of the unfinished index. Recognizing the scholarly value of an MQ index, and sharing the late Archibald’s twin interests in librarianship and the history of mathematics, Tattersall had the idea to complete the project, and even improve on it by incorporating the ET. The task was immense, since MQ had run for 110 issues and the ET for 75 issues. In the final count, the total number of mathematical questions and solutions was in the tens of thousands. Nevertheless, Tattersall pursued the project. He built his index in the form of a series of tables, created with the aid of computer software. Thus the index transitioned from physical to digital media. Tattersall eventually shared his tables with Dr. Sloan Despeaux, another historian of mathematics, and they discussed the idea of publishing the tables as an online database, so that scholars around the world could make use of them. The indexing project was an ambitious idea, which has been carried out collaboratively across multiple generations of mathematicians.
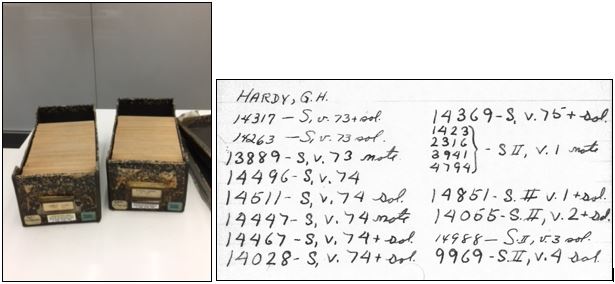
Figure 11. Two boxes, with a sample card, of the file cards created by Archibald in the 1940s–50s and discovered
years later by Tattersall in the Brown University Science Library. Images courtesy of James Tattersall.
Robert M. Manzo (University of North Carolina at Chapel Hill), "The Educational Times Database: Indexing MQ and ET’s Mathematical Problems, 1940s–2000s," Convergence (March 2021)




