- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Mathematical Cultures of Medieval Europe - The Mathematics of the Jews
There was a significant Jewish community in Spain under Muslim rule and, in many times and places, Jews could integrate into the Muslim society. They often served the rulers in administrative or financial capacities. The Jews became fluent in Arabic and used this language in their intellectual pursuits. However, I am not aware of any mathematical work by Jews until the late eleventh century, by which time Toledo and many other parts of Spain were already in Christian hands. We should emphasize that when Jews were living closed off from their neighbors, their creativity was mainly displayed in interpretations of the Bible and of Jewish law. But once Jews could participate in the general society, as in this time period in Spain, they started to display creativity in other fields, including mathematics.
One of the first known Jewish mathematicians is Abraham bar Ḥiyya of Barcelona (1070-1145), who was a community leader as well as a scholar. His Jewish title was nasi (honorary leader), while his Arabic title was ṣāḥib ash-shurṭa (head of the guard, transliterated in Latin as “Savasorda”), a title he probably received from the ibn Hūd dynasty in Saragossa, where he spent time before that dynasty was overthrown. He wrote on mathematics, astronomy, astrology and philosophy, and is distinguished as the first Jewish scholar in the Arabic speaking world to write on science in Hebrew. This choice of language was, at least in part, due to the lack of access of Jews in Provence, where he visited, to the Arabic language. His work includes translations from Arabic to Hebrew, and he collaborated with Plato of Tivoli on translations into Latin as well.
Bar Ḥiyya’s most important mathematical work was The Treatise of Measuring Areas and Volumes. This book was partially translated into Latin in 1145 by Plato of Tivoli, perhaps with Abraham’s help, and made an impact on European scholarship. The treatise opens with a motivational introduction, stating explicitly that Abraham wrote the book to teach the appropriate geometry necessary for both secular and holy affairs. After presenting versions of the early books of Euclid’s Elements, Abraham proceeded to deal with measurements of squares, rectangles and rhomboids (deriving their areas, sides, diagonals, etc. from each other), and included a geometric treatment of quadratic problems. He continued on to triangles, general quadrilaterals, and circles and then studied measurement of polygons by triangulation before presenting some practical suggestions for measuring sloping and curved lands. There is then a section on division of plane areas, perhaps based on Euclid’s own no longer extant book on the same topic.
This work is not a full scholarly geometry, but a compromise between an introduction to abstract geometry and a measurement manual. It provides a good intuitive introduction to geometrical reasoning and has some problems like those of ibn ‘Abdūn. As we will see later, Leonardo of Pisa seems to have used this book, probably in the Latin translation, as one of the sources of his Practical Geometry. But also, it seems clear that in Abraham’s time, Jews generally did not study abstract subjects. If they were interested in mathematics at all, they tended to concentrate on practical subjects.
We begin with Abraham’s motivations for studying geometry at all:
[The scriptures say] “I the Lord am your God, instructing you for your own benefit, guiding you in the way you should go” (Isaiah 48:17), that is, instructing you in whatever is useful for you, and guiding you on the way you follow, the way of the Torah. From which you learn that any craft and branch of wisdom that benefit man in worldly and holy matters are worthy of being studied and practiced.
I have seen that arithmetic and geometry are such branches of wisdom, and are useful for many tasks involved in the laws and commandments of the Torah. We found many scriptures that require them, such as “In buying from your neighbor, you shall deduct only for the number of years since the jubilee”, and “the more such years, the higher the price you pay; the fewer such years, the lower the price”, followed by: “Do not wrong one another, but fear your God” (Leviticus 25:15-17). But no man can calculate precisely without falsification unless he learn arithmetic. … Moreover, the Torah requires geometry in measuring and dividing land, in Sabbath enclosures and other commandments. … But he who has no knowledge and practice in geometry cannot measure and divide land truly and justly without falsification. … It suffices to note that the blessed God prides himself in this wisdom, as is written: “He stood, and measured the earth” (Habakkuk 3:6) and “Who measured the waters with the hollow of His hand, and gauged the skies with a span” (Isaiah 40:12). So, you see from these writings that the blessed God created his world in well founded and weighed out measurement and proportion. And a man must be like his creator with all his might to win praise, as all scholars agree, so from all this you see the dignity of these branches of wisdom. He who practices them does not practice something vain, but something useful for worldly and holy matters.
Arithmetic, which is useful for worldly matters and crafts as well as for the practice of many commandments, is not difficult to understand, and most people understand it somewhat and practice it, so one does not need to write about it in the holy tongue. Geometry is also as useful for as many matters as arithmetic in worldly matters and commandments from the Torah, but is difficult to understand, and is puzzling to most people, so one has to study and interpret it for land measurement and division between heirs and partners, so much so that no one can measure and divide land rightfully and truthfully unless they depend on this wisdom.
I have seen that most contemporary scholars in Spain and Provence are not skillful in measuring land and do not divide it cleverly. They severely belittle these matters, and divide land between heirs and partners by estimate and exaggeration, and are thus guilty of sin … Their calculation might mete out a quarter to the owner of a third, and a third to the owner of a quarter, and there is no greater theft and falsification. [Katz et al, 2016, 297-298]
Although there are many occasions in the Talmud where approximations are used, Abraham insisted that
Our fathers did not allow us to dismiss calculations, nor steal from heirs, nor give any of them more or less than their fair share …. They warned us and gave us strict orders against stealing and falsifying in measuring land ... [Katz et al, 2016, 298-299]
Thus, Abraham concluded, one needs to study the principles of measurement carefully, so that one calculates shares of heirs correctly. So, unlike ibn ‘Abdūn, Abraham presented careful proofs of his rules for calculation, generally based on the Elements. Consider the following examples:
A square quadrilateral that you take away from the number of its area the number of its four sides, and are left with 21 cubits of its area: what is the area and what is the number of each side of the square? Answer: Divide the number of the sides, which is four, into two. Multiply the two by itself, which is 4. Add this number to the given number that’s left over from the square, and the total is 25. Find the root of 25, which is 5. Add half the sides, which is 2, so the total is 7. This is the side of the square, and its area is 49. He who posed the question subtracted from the area, which is 49, the number of the four sides, each of which is 7 and all four 28, leaving from the square 21, as he told you. [Katz et al, 2016, 300-301]

Figure 4. Bar Ḥiyya’s diagram of a square used to justify an algorithm for calculation
After presenting this algorithm, bar Ḥiyya drew a diagram of the square ABCD, then subtracted off rectangle BEGC with BE of length 4 (i.e., the four sides), leaving a rectangle EADG of area 21. He then divided BE in half at H and quoted Elements II-6 to conclude that the square on HA is the sum of rectangle EADG and the square on HE, that is 25. Therefore, HA itself equals 5 and AB equals 7, as desired.

Figure 5. Circle and triangle used to derive a circle area formula
To measure a circle, Abraham presented the classical result that the area was half the diameter times half the circumference. His proof, depending on decomposing an area into lines that it contains, is evidently original:
We know that if you open the area of the circle on one side, and straighten all the surrounding lines from the external line [circumference] to the center, the lines surrounding the area of the circle will spread and turn into straight lines, decreasing until they turn into a single point, which is the center point. Such is the line ABCD … that I have drawn, where the external is the largest, and the next is smaller than the former but larger than the next, and so on to a point, which creates the form of a triangle. But we have already taught the area of a triangle, which is as the height times half the base, which is half the diameter times half the circumference. [Katz et al, 2016, 306]
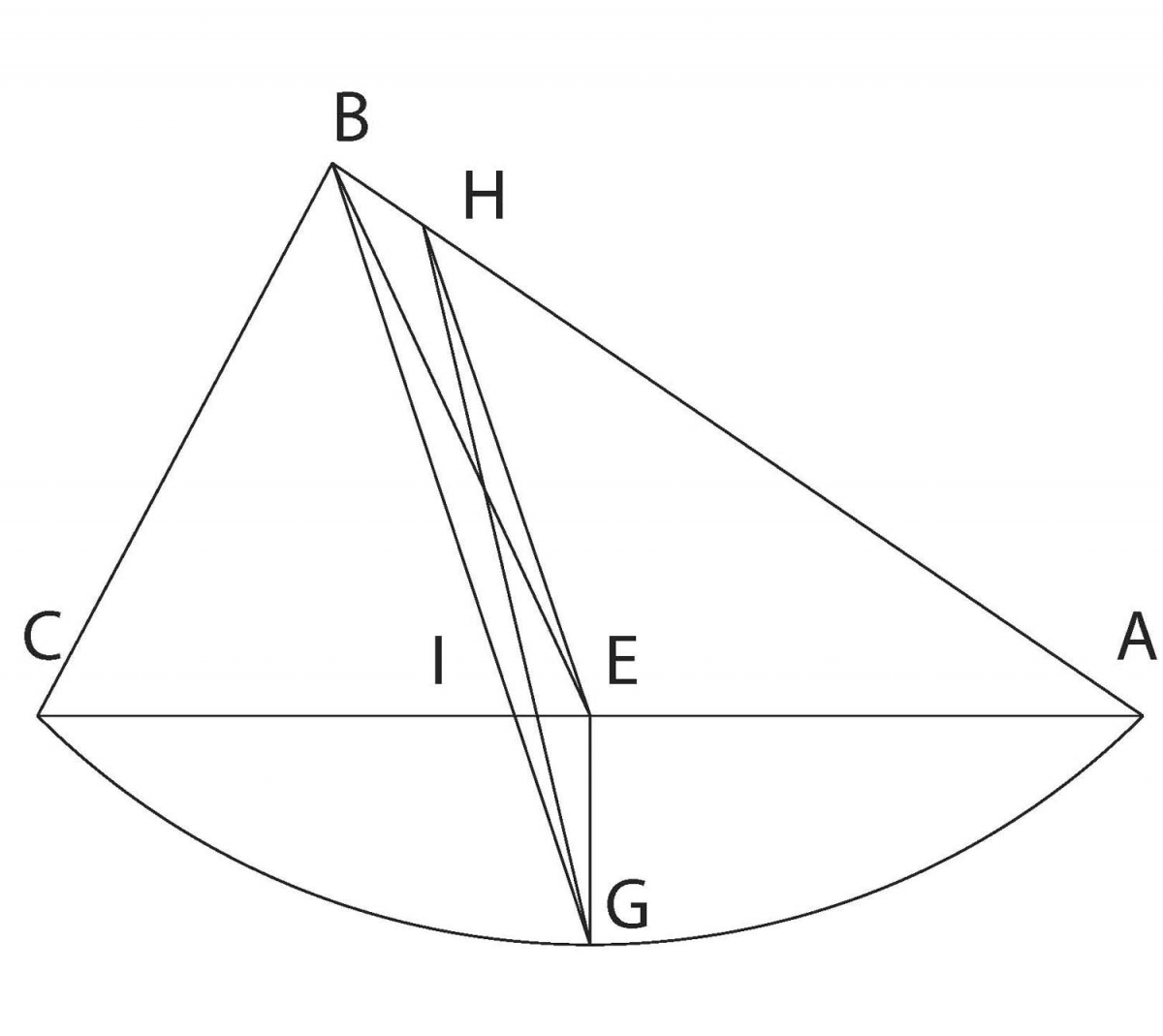
Figure 6. Diagram used to divide a region in half
As an example of dividing fields, Abraham began with a region bounded by an arc of a circle and two straight lines, neither of which are radii. His goal was to find a straight line dividing the region in half. Here E is the midpoint of line AC and EG is perpendicular to AC. Line BG intersects AC at I; then HE is drawn parallel to BG. Then GH divides the region in half. To prove the result, note that BE divides triangle ABC in half, while EG divides segment AECG in half. But triangles GHE and BHE are equal. It follows that region AHG is equal to the sum of triangle ABE and region AEG, so is half of the entire region ABCG.
Abraham ibn Ezra (1090-1167) was a younger contemporary of Abraham bar Ḥiyya. He was born in Tudela, when it was part of the kingdom of Saragossa, but then traveled widely during his adult life. Among his numerous works were books on arithmetic and numerology, as well as a work dealing with astrology which had some interesting combinatorial aspects. As he wrote,
Only when one knows the natural sciences and their proofs, learns the categories that are the ‘guardians of the walls’ taught by the science of logic, masters the science of astronomy with its absolute proofs based on mathematical knowledge, and comprehends the science of geometry and the science of proportions, can one ascend to the great level of knowing the secret of the soul, the secret of the supernal angels, and the concept of the world to come in the Torah, the Prophets, and the sages of the Talmud [Ibn Ezra, 1995, chap. 1].
In other words, the reason for studying mathematics was ultimately to get closer to God. Thus, in general, that mathematics could be studied that was useful toward that end.
In his Sefer ha-Mispar (Book of Number), ibn Ezra expounded on “the science of proportions” as he showed how to use the rule of three to solve problems. He began with methods of calculation, in which he explained the Hindu-Arabic number system, although with Hebrew characters for the digits. But he then showed how to solve numerous commercial problems, such as
Reuven hired Simon to carry on his beast of burden 13 measures of wheat over 17 miles for a payment of 19 pashuts. He carried seven measures over 11 miles. How much shall be paid? [Katz et al. 2016, 231]
Another of the subjects that ibn Ezra thought was useful was astrology. He wrote a series of books on the subject. In particular, in Sefer Haʿolam (Book of the World), ibn Ezra discussed the meaning of celestial conjunctions and aspects. He began by counting all possible conjunctions of the seven known planets, demonstrating some systematic combinatorial reasoning. In order to calculate the number of different sets of n elements out of 7 planets, he used a recursive method, taking partial sums of the sequence 1,2,3,4,5,6,7, then taking partial sums of the sequence of these partial sums, etc.
There are 120 conjunctions [of the seven planets]. You can calculate their number in the following manner: it is known that you can calculate the number that is the sum [of all the whole numbers] from one to any other number you wish by multiplying this number by [the sum of] half its value plus one-half. As an illustration, [suppose] we want to find the sum [of all the whole numbers] from 1 to 20. We multiply 20 by [the sum of] half its value, which is 10, plus one-half, and this yields the number 210. We begin by finding the number of double conjunctions, meaning the combinations of only two planets. It is known that there are seven planets. Thus, Saturn has 6 [double] conjunctions with the other planets. [Jupiter has 5 double conjunctions with its lower planets, Mars has 4, and so on. So we need to add the numbers from 1 to 6]. Hence, we multiply 6 by [the sum of] half its value plus one-half, and the result is 21, and this is the number of double conjunctions. [Katz et al, 2016, 271-272]
Ibn Ezra next found the triple conjunctions, effectively showing that \[C_{7,3}= C_{6,2}+ C_{5,2} +C_{4,2}+ C_{3,2}+ C_{2,2},\] where each \(C_{k,2}\) is shown to be the sum of integers up to \(k-1.\) (For a classroom activity in which students discover this formula, see the Convergence article, "Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom.") Ibn Ezra continued in this manner with quadruple conjunctions and so on until he had found the total of 120 indicated above.
In a further work, the Book of Measure, ibn Ezra gave without proof numerous procedures for determining areas of geometrical figures. Many of these are like material found in bar Hiyya’s work, such as the following problems:
We have added the sides and the area; this gives so much. How much is the side? Take the square of half the number of all the sides [= 4] and add it to the sum [of the area plus the four sides]; subtract from the root of this result half the number of the sides [= 2].
Or, for the circle: If one is dealing with a semicircle, its area is like that of half a circle. If it is smaller or larger [than a semicircle], you must know the diameter of the circle from which the circular segment has been cut, and the length of the chord of the arc and of the sagitta. When you know two of these [three] elements, you can determine the third. Problem: The chord is 8, the diameter, 10. How much is the sagitta? Subtract from the square of half the diameter the square of half the chord; take the root of the remainder, and subtract it from half the diameter; you will find the sagitta [= 2]. [Katz et al, 2016, 289, 291]
Ibn Ezra also presented a table of Sines and later displayed the standard medieval method of using an astrolabe to calculate heights and distances. If one knows the distance to the tall object whose height is to be measured, one uses the astrolabe to measure the proportion of height to distance, from which the height can be calculated. If one does not know the distance, one takes two measurements with the astrolabe from different places and then uses a formula known in China and elsewhere for centuries to calculate the height.
Although ibn Ezra had stated the reasons one could study the sciences, he was not the only one. Baḥya ibn Paqûda, a Jewish philosopher from Saragossa in the mid-eleventh century, wrote the following in his Duties of the hearts:
All departments of science, according to their respective subjects, are gates which the Creator has opened to rational beings, so that they may attain to a comprehension of revealed religion and of the world. But while some sciences satisfy primarily the needs of religion, others are more requisite for the benefit of the world. The sciences specially required for the affairs of the world are the lowest division – namely the science that deals with the natures and accidental properties of physical substances – and the intermediate division – namely the science of mathematics. These two branches of knowledge afford instruction concerning the secrets of the physical world and the uses and benefits to be derived from it, as well as concerning arts and artifices needed for physical and material well-being. But the science that is needed primarily for revealed religion is the highest science, namely the divine science, which we are under obligation to study in order to understand our revealed religion and to reach up to it. To study it, however, for the sake of worldly advantages is forbidden to us. [Freudenthal, 1995, 34]
It was Spanish-born Maimonides (1135-1204), however, whose work was much more important in influencing Jews to study science. Maimonides' family left Spain for North Africa during the reign of the Almohads, but simply settled in another part of the Almohad empire there. Eventually, he traveled to Palestine and then spent the rest of his life in Egypt as a physician to the sultan as well as the most important philosopher in Jewish history. For Maimonides, the study of science and philosophy was actually a religious obligation:
It is certainly necessary for whoever wishes to achieve human perfection to train himself first in the art of logic, then in the mathematical sciences according to the proper order, then in the natural sciences, and after that in the divine science [Freudenthal, 1995, 32].
Maimonides emphasized that it was only truth that counted, and that it did not matter who discovered it. On the other hand, since it was the “divine science” of metaphysics that was the ultimate goal, Maimonides emphasized that science was legitimate and desirable only in so far as it contributed to the divine science. Thus, Medieval Jews were to study mathematics either because they regarded it as essential for metaphysics, preparing the intellect to apprehend abstract truths, or because they needed it as a prerequisite for the study of mathematical astronomy, important for calculating the calendar.
It seemed clear that the study of Euclid’s Elements was legitimate, and indeed it was widely and continuously studied. Trigonometry, which the Jews learned from the Muslims but to which they made contributions as well, was also a valued study. But somehow, at least in the eleventh and twelfth centuries, it was argued that the study of algebra was pointless, indeed harmful. Medieval algebra was construed as a mere technique, allowing one to solve equations, and as such it had no philosophical value, nor was it apparently of practical use. Abraham ibn Daud of Toledo (1110-1180) wrote:
Among those who spend their time on vanities, thereby depriving their soul of afterlife, is he who consumes his time with number and with strange stories like the following: A man wanted to boil fifteen quarters of new wine so that it be reduced to a third. He boiled it until a quarter thereof departed, whereupon two quarters of the remaining wine were spilled; he again boiled it until a quarter vanished in the fire, whereupon two quarters of the rest were spilled. What is the proportion between the quantity obtained and the quantity sought? [Freudenthal, 1995, 37]
Maimonides himself wrote that the books on conics and on devices (i.e. algebra) and on the science of weights were instances of inquiries that must not be pursued as ends in themselves. They were only worth studying if they helped to “sharpen the intellect” in order to help man achieve knowledge of God. Interestingly, Maimonides himself drew on the demonstrated existence of asymptotes to show that imaginability is not a criterion of existence. “Hear what the mathematical sciences have taught us and how capital are the premises we have obtained from them” [Freudenthal, 1995, 37].

Figure 7. A street sign honoring "Rabi Levi ben Gershom," also known by the acronym "Ralbag"
The foremost medieval Jewish mathematician, Levi ben Gershon (1288-1344), certainly read Maimonides’ works. Yet he interpreted Maimonides differently from most others. Namely, he felt there should be no restriction on what he could write about in science or in mathematics. Because all knowledge of God’s works has religious significance, the acquisition of scientific knowledge about the world is a legitimate end in itself. Thus, Levi explored many different aspects of science and mathematics.
His earliest mathematical work was the Ma’ase Ḥoshev (The Art of the Calculator), a book using Euclidean methodology and, in essence, mathematical induction to prove numerous results in number theory and combinatorics. The first part of the book is very abstract. The earlier propositions deal with such topics as summing integers or squares, while the concluding ones contain important results in combinatorics. Some of the results appear unusual at first glance, such as the following:
To find three numbers such that the sum of the first and third contains the second as a factor as many times as a given number and such that the sum of the second and third contains the first as a factor as many times as a second given number [Katz et al, 2016, 259].
Presumably, this result was included because, in the problem section of the text, Levi wanted to include a numerical version of this challenge and because this is an abstract version of a problem that had appeared earlier in Latin mathematics as the problem of men finding a purse. Also, Levi probably wanted to present combinatorial results because Jews had for centuries been interested in such questions as how many possible words could be formed with the letters of the Hebrew alphabet. Now Levi did not answer such a question directly, but just presented results about combinations and permutations of sets of objects, often proved using what we know as mathematical induction. For example,
When you are given a number of terms and the number of permutations of a second given number from these terms is a third given number, then the number of permutations of the number following the second given number from these terms is the product of the given third number by the excess of the first given number over the second number [Katz et al, 2016, 274].
In modern terms, this result says that \(P_{m,n+1}=(m-n)P_{m,n}.\) This is the inductive step for proving that \[ P_{m,n}=m(m – 1)(m – 2)\cdots(m – k + 1),\] a theorem Levi stated next:
And so, it is clear that the permutations of a given number from a second given number of terms is equal to the number built from consecutive numbers. Their number is equal to the first given number, and the last one is the second given number. [Katz et al, 2016, 275]
(For more problems from Levi ben Gershon's Ma’ase Ḥoshev, see the Convergence article, "The Mathematics of Levi ben Gerson in the Classroom.")
Levi wrote several other mathematical works, two of which were quite theoretical. One of these was a commentary on Euclid’s Elements, in which he spent quite a bit of time giving a proof of Euclid’s parallel postulate. His argument was quite rigorous, but he began with a different postulate:
The straight line which is inclined [to another straight line] approaches [the second line] on the side where an acute angle is formed [with a line crossing both of these that is a perpendicular from the first line to the second] [Katz et al, 2016, 328].
He also wrote a number theory work at the request of a French music theorist. Here he gave a very clever proof of the theorem that a power of 2 must differ from a power of 3 by at least 2, except in the cases 1,2; 2,3; 3,4; and 8,9 [Katz et al, 2016, 277-283]. Presumably this result was of use in music theory, but it is not clear how this would meet Maimonides’ criteria for what could be studied.
There were a few other Jewish mathematicians in Spain and France who also ignored Maimonides’ strictures. For example, consider the work of Abner of Burgos (1270-1348), who lived in Castile. He was originally a Jew, but converted to Christianity and was then known as Alfonso di Valladolid. His most important mathematical work is the Sefer Meyasher ‛aqov (Book of the Rectifying of the Curved), whose aim is to enquire whether there possibly exists a rectilinear area equal to a circular area truly and not by way of approximation. Unfortunately, in the only manuscript we have, the concluding chapter, where the aim was to be accomplished, is missing. But it is the third chapter in which Alfonso considered many interesting geometrical questions related to curves and solids. In particular, Alfonso defined and used the "conchoid of Nicomedes." It is usually accepted that interest in Nicomedes’ work – and his original treatise is lost – was only revived in the late sixteenth century, when it was mentioned and used by Viéte and then later by Descartes and Newton, among others. But, in fact, this curve was discussed by Alfonso, with some important applications. So, what is the conchoid?
Given a straight line (the “ruler” or “canon” AB), a point outside it (the “pole” P), and a distance b, the conchoid of Nicomedes is the locus of all points lying at the given distance d from the ruler AB along the segment that connects them to the pole P. If P is the origin, and AB the line y = a, then the curve is defined by the polar equation r = a sec θ + b. The curve has two branches on opposite sides of the ruler, to which both are asymptotes. The branch passing on the side of the pole has three different distinct forms, depending on the relationship between a and b: If a < b, it has a loop; if a = b, then P is a cusp point; and if a > b, the curve is smooth. The other branch does not change topologically. All versions are shown in the link above.
The importance of the curve to Nicomedes, and later to European mathematicians, was that its use allowed the trisection of an angle, the construction of two mean proportionals between two given line segments, and the doubling of the cube. Alfonso, in fact, demonstrated each of these. His angle trisection is similar, but not identical, to that attributed to Nicomedes, but his construction of two mean proportionals is not found in any of the Greek or Arabic literature, and his use of this to construct the doubled cube is unique. In fact, he constructed a generalization of the Delian problem: To construct a polyhedron which is equal in volume to a given polyhedron and which is similar to a second given polyhedron. To get the doubled cube, simply assume the first given polyhedron is any parallelepiped of volume 2, while the second one is a cube of volume 1. For details, see [Katz et al, 2016, 347-353].
Somewhat later, we find Isaac ibn al-Ahdab (1350-1430) and Simon Motot (mid-fifteenth century) actually studying and writing about algebra. The former was born in Castile, but ended up in Sicily after leaving Spain. He studied the algebra of the Maghrebian mathematician Ahmad ibn al-Banna’ and wrote a detailed commentary on it [Wartenberg, 2015]. Motot lived in Italy and probably learned his algebra in the Italian abacus tradition of his time. His treatise was the first original Hebrew work giving a detailed treatment of the al-Khwārizmīan form of algebra.
Still Levi was, without doubt, the most accomplished Jewish mathematician of the Middle Ages. Even though he went beyond the standard interpretation of Maimonides in deciding that he could study and write on any topic he thought interesting, there were few followers. There was a conflict within the Jewish community regarding what subjects could legitimately be studied, with a sizable proportion of “traditionalists” insisting that only the Torah and Talmud were worthy of study. A further issue was that there was no institutional infrastructure for new students to learn the works of their predecessors. One could always arrange to study privately with an individual, and certainly there were “study groups” established by various people, including Levi himself. But there were no Jewish universities – just as there were no Muslim universities.
Leon Joseph of Carcassonne, who lived around the turn of the 14th-15th centuries in the south of France, wrote about this very issue:
Many years ago I directed my attention toward the study of and research into the profane sciences, which are several in number and nature…. In my eyes, the merits of these sciences were above all praise. ... I therefore followed in the footsteps of the learned men of our own times, … so that they should illuminate my way with the light of their intelligence and understanding …. But I realized that the lack of knowledge that they, and some of my people at this time, found themselves submerged in was great and immense … I perceived that said lack of knowledge on the part of one sector of our nation was by no means strange. Its cause was not unknown and I was not unaware of the Talmudic law which referred to it … Then I heard a voice telling me that there was not one single cause, but many, for the lack and absence of this knowledge among some of our scholars. Sciences defeated them because their subject matter is more rational than in the bosom of our people, and they are as far from them as east is from west, and all the more so from the fundamentals of the Torah and of religious faith. [Those few who did study the sciences] had no right to propound [their knowledge] in the squares and streets, or to discuss it, to show themselves to be favorable toward it, nor to conduct public debates with the aim of reading the complete truth, for knowledge of the truth can only be attained by means of the contrary. …
On seeing the obstacle that these causes represented and aware that the aforementioned sciences were known among the Christians, I said to myself: I shall study their language a little. I shall attend their schools and houses of study. I shall follow their footsteps so that I am able to make use of whatever I might learn from their words. … I found great benefits in this, because in general their discussions on these sciences do not stray from the subject matter; they leave out nothing when it is a question of debating the truth or falsehood of a proposition; they are very rigorous concerning the questions and answers of a debate, which are linked together in such a way as eventually to bring out the truth by means of an analysis of opposing points of view "like a lily among thorns." The way of studying that they practice today as regards these sciences is the same as that followed by our own scholars in earlier times in their study of the science of the Torah. … If these and other sciences should remain beyond our reach, it is not because our intelligence is inferior to that of the Christians, for we possess the same capacity for understanding; indeed, it is the circumstances that have kept us apart, and the memory of them has been erased as a result of exile and repression, and in the same way their pleasure, splendor, and wealth [have been erased]. For this reason, the Christians have continued to advance in the profane sciences while we have continued to lose ground as a consequence of distress and oppression. [Garcia-Ballester et al, 1990, 106-110]
Victor J. Katz (University of the District of Columbia), "The Mathematical Cultures of Medieval Europe - The Mathematics of the Jews," Convergence (December 2017)




