- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Curved Figures
The most interesting problems with quadrature deal with figures having curved sides, the quintessential example being the quadrature of the circle. Today, we express our knowledge about the quadrature of the circle through the familiar area formula A = \(\pi\)r2 where r represents the radius of the circle. We can also use a less familiar but equivalent (and useful) formula A = [\(\pi\) /4]d2, where d is the circle's diameter. But the simplicity of the formulas masks the underlying conceptual difficulties. The formulas make clear that the area of a circle is a certain multiple of the area of the square whose side is the radius (or, respectively, the diameter) of the circle, so an immediate connection to quadrature is made. This relationship can be made even clearer by expressing the area formula as
|
This brings forward the fact that the ratio between the area of the circle and the area of the square on its radius (or its diameter) is a constant value, independent of how large or small the circle is. This constant ratio between area of the circle and the area of the square on its radius we have recognized to be so important a constant that we have given it a special name, \(\pi\).30 But giving the number a special symbol gives no indication of its value. What is this number \(\pi\)?
Ancient pre-Greek mathematicians dealt with the area problem for the circle in various ways, but nearly all of these presented solutions that were at best good approximations to an exact quadrature. For instance, the Rhind Papyrus from Egypt (a 17th century BCE copy of a 19th century original) records that a circle is equal to the square on 8/9 its diameter. This is equivalent to saying that \(\pi\) = 256/81 = 3.16049..., a bit larger than it should be. In the Hebrew Scriptures, in the first Book of Kings, we read about the construction of the ceremonial bowl that was erected at Solomon's Temple in Jerusalem (1 Kgs 7:23) that it was to be 10 cubits across and 30 cubits around, giving a value of \(\pi\) = 3, which is too small. This latter was a very commonly used approximation, no doubt for its simplicity, and was used in Babylonia as well. In the Indian Sulvasutras, the main source for ancient Indian mathematics prior to the seventh century BCE, we find the following verse:
If you wish to turn a circle into a square, divide the diameter into 8 parts, and again one of these eight parts into 29 parts; of these 29 parts, remove 28, and moreover the sixth part (of the one part left) less the eighth part (of the sixth part).
The Brahmin author means to say that the area of the circle is equal to the area of a square whose side is a certain fraction of the diameter of the circle, that fraction being
|
which is equivalent to having \(\pi\) = 3.0883...
The problem of the quadrature of the circle is an old and thorny problem, so much so that, to this day, we use the phrase "squaring the circle" to refer to any intractable problem.
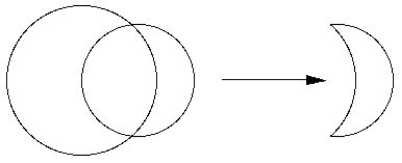
Toward the end of the fifth century BCE, Hippocrates of Chios,31 a geometer of considerable prowess, lived and taught in Athens. As for many other figures in the ancient world, we know very little about his life. Over 800 years later, the historian Proclus reported that Hippocrates was the first to write a work on elements of geometry. Indeed, there is evidence to suggest that Hippocrates may have been the source for much of what eventually was included by Euclid in his Elements when it was written some 100 years or so later. Our main interest in Hippocrates here is his discovery of the quadrature of certain lunes. We will learn how he did this by consulting two short excerpts from other historians of geometry who wrote some centuries later; none of his own writings survive today.
Footnotes:
30It may be surprising to learn that, despite the fact that we use a Greek letter to represent this number, the use of the letter \(\pi\) for this number does not come to us from the Greeks. The first use of the symbol (the first letter of the Greek word periphereia, meaning circumference, from the related fact that it is also the ratio of the circumference to the diameter of any circle) dates to the early eighteenth century in Britain, and was popularized by the noted Swiss mathematician Leonhard Euler .
31Do not confuse him with Hippocrates of Cos, a comtemporary, but renowned as a physician. It is this second Hippocrates for whom the famous oath of physicians, to above all do no harm to their patients, is named. Both Cos and Chios are islands in the Aegean Sea.
Daniel E. Otero (Xavier University), "The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Curved Figures," Convergence (July 2010)




