- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Thomas Simpson and Maxima and Minima - Motion of bodies I
Two bodies move at the same time, from two given places A and B, and proceed uniformly from thence in given directions, AP and BQ, with celerities in a given ratio; it is proposed to find their position, and how far each has gone, when they are nearest possible to each other (Example XIII, page 28).
Let \(a = AC, b = BC, c = DC\) in the adjacent figure. Assume \(m\) is the velocity (“celerity”) of the body that moves in the direction \(AP\) while \(n\) is the velocity of the body that moves in the direction \(BN\).
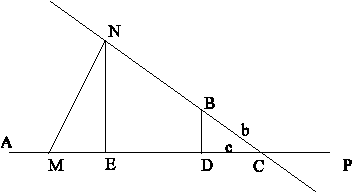
At time \(t\) the first body will be at \(M\) while the second body will be at \(N\) (Simpson calls these two points “cotemporary”). Next draw perpendiculars \(\overline{NE}\) and \(\overline{BD}\) to \(AP\), and let \(x = CN\). Since \(\triangle ECN\) is similar to \(\triangle DCB\), we can conclude that \(\frac{b}{x} = \frac{c}{CE}\). Because \(M\) and \(N\) are cotemporary points it follows that \(\frac{AM}{m} = \frac{BN}{n}\), therefore \(AM = \frac{m}{n}(x - b)\). So \(CM = AC - AM = a - \frac{m}{n}(x - b) = d - \frac{m}{n}x\), where \(d = a + \frac{m}{n}b\). By the law of cosines we have \(MN^2 = CM^2 + CN^2 - 2(CM)(CN)cosC\). But \(cosC = \frac{EC}{CN}\). Therefore
\(MN^2 = CM^2 + CN^2 - 2(CM)(CE) = (d - \frac{m}{n} x)^2 + x^2 - 2(d - \frac{m}{n} x) \frac{cx}{b}\)
\(= d^2 - (\frac{2dm}{n} - \frac{2cd}{b}) x + (\frac{m^2}{n^2} + \frac{2cm}{nb}) x^2\).
Taking the derivative of \(MN^2\), which is obviously a function of \(x\), and making it equal to zero we get
\(x = \frac{mnbd + cdn^2}{bm^2 + 2cmn}\)
This is the value where \(MN^2\), and consequently \(MN\), attains its minimum.
Remark: Maybe Simpson should have mentioned that \(MN^2\) is a second degree polynomial in the variable \(x\), thus on the Cartesian plane it represents a vertical parabola that opens upwards with minimum at \(-\frac{r}{2s}\) where \(r\) and \(s\) are the coefficients of \(x\) and \(x^2\) respectively. We would get exactly the same value obtained before, namely
\(x = \frac{mnbd + cdn^2}{bm^2 + 2cmn}\)
So, in this problem there is an alternative to the use of derivatives.
Editor’s Note: This article was published in 2005.
Michel Helfgott, "Thomas Simpson and Maxima and Minima - Motion of bodies I," Convergence (August 2010)




