- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Logistic Growth Model - Fitting a Logistic Model to Data, II
In the preceding part, we determined the reasonableness of a logistic fit (up to 1940) and estimated the parameters r and K using only the differential equation, not the symbolic solution found in Part 5. Now we see what we can do by using the solution, which we recall has the form
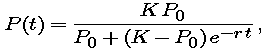
where P0 is the population at whatever time we declare to be time 0. For example, if t = 0 in 1790, then P0 = 3.929. For purposes of this exercise, we will make that choice of starting point and measure all times from 1790.
- First, examine the solution with the parameters r and K from Part 6 by plotting the solution formula together with the data through 1940. (Don't worry if the fit is not very good -- we will see another way to estimate the parameters in the next two steps.)
In Part 5, as a step on the way to the symbolic solution, we saw that the solution would have to satisfy
that is, ln (P / (K - P)) should be a linear function of t with slope r. Thus, given a value of K, we can plot ln (P / (K - P)) against t and see if we get a straight line. (Note that there is no need to approximate rates of change for this type of test.) Since you already have an estimate of K from Part 6, it will not be a surprise if the plot looks pretty straight on the first try.
- Use the commands in your worksheet to test the data for this type of fit. If your plot does not appear to be sufficiently straight, adjust K, recompute the data, and replot until you are satisfied that the plot is as straight as you can make it.
- From the approximately linear relationship between
ln (P / (K - P)) and t in step 2, make a new estimate of r.
- Replot your solution formula, along with the data, using your new value of r (and your new value of K if you changed it). If your plot is not yet satisfactory, repeat steps 2 and 3 until you are satisfied that you have the best values for K and r that you can get.
Leonard Lipkin and David Smith, "Logistic Growth Model - Fitting a Logistic Model to Data, II," Convergence (December 2004)




