- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Raindrops - Background: Falling Bodies
Our models for velocity of a falling object will all be based on Newton's Second Law of Motion, which states that force equals mass times acceleration:

Here F is the force exerted on an object of mass m, causing the object to have an acceleration a.
Acceleration is defined to be the derivative of velocity, i.e.,

where v = v(t) is the velocity at time t. Thus Newton's Law can be rewritten as
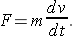
The primary force on a falling body is gravity, the pull of the Earth's mass on the object. Our first model for a falling body will consider gravity to be the only force on the object.
It is known through experimental observation that (near the surface of the Earth) the force of gravity on an object is proportional to the mass of the object, i.e., there is a constant g such that

The value of the constant g is known by experimentation to be approximately 32.2 sec2.
Equating our two formulas for the force F and dividing by m, we find a differential equation:
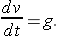
-
Make a mental image of what this differential equation says -- what its slope field looks like, and what its solutions look like. Then execute the relevant commands in your worksheet to confirm your image.
If we assume that our object was initially at rest at time t = 0, then our initial condition is
v(0) = 0. Together with the differential equation, we have an initial value problem for the velocity function v = v(t):

- Enter the solution of this initial value problem in your worksheet.
This solution for a velocity function leads to a second differential equation: The velocity v is itself the derivative of the distance function s = s(t), i.e.,

- Substitute your formula for v into this equation, and construct a slope field for this differential equation. Does it have the appearance you expect?
- Write down an appropriate initial condition for s. What is the solution of this initial value problem?
- Using this model for distance as a function of time, compute how long (in seconds) it would take a raindrop to fall from a height of 3000 feet. How fast would it be traveling when it hit the ground? Give your answer first in feet per second, and then convert it to miles per hour.
- What would happen if you got hit with a raindrop traveling at this speed? Is this consistent with your experience with rain?
David A. Smith and Lawrence C. Moore, "Raindrops - Background: Falling Bodies," Convergence (December 2004)




