- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Technology in the Upper-Level Curriculum - Real Analysis
When I had taught real analysis previously, I had been frustrated by the students' lack of understanding of this very abstract material. So I was eager to see how technology could be used to help students grasp these difficult concepts. In the spring of 1999, I taught real analysis using the computer algebra system Mathematica. I planned the course around six or seven standard topics from real analysis and used a standard, formal text. Each topic was to be covered using the format of an introductory discovery session in the lab, classroom discussion with formalism introduced, and a final class session where students presented solutions to problems.
In the early part of the semester, the classroom sessions were challenging and enlightening for the students, but I was having limited success in connecting their intuitive ideas, developed in beginning calculus, to the formalism of the real analysis text. By mid-semester, it was clear that the discovery approach in the laboratories -- which had been so successful in abstract algebra -- was not working well. Fortunately, the students were comfortable articulating their frustrations in a long classroom discussion. Although the computer-generated examples enhanced their intuitive understanding of topics they had learned in calculus, they told me that they definitely had no idea of how this intuition related to the formalism that I had been emphasizing in the classroom.
![]() During the next class, I wrote a simple
During the next class, I wrote a simple 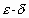 proof on the board, and I also projected the computer screen with the Mathematica information generated in their lab: the familiar graph showing the
proof on the board, and I also projected the computer screen with the Mathematica information generated in their lab: the familiar graph showing the ![]() and related
and related ![]() , and a table of numerical values for
, and a table of numerical values for ![]() 's and
's and ![]() 's. In the formal example I used, the computations for the proof implied that
's. In the formal example I used, the computations for the proof implied that ![]() , and the numerical tables showed this as well. [To download the original Mathematica notebook, click on the icon to the right. The "example" link shows the same information in a browser window.] The formal proof, the graph, and the numerical tables were all in front of the students at once -- I had to move between these various presentations of the same concept several times. Finally, one by one, the students’ faces signaled understanding. They had grasped the meaning of the formal mathematical proof, but only after they had seen the visual and numerical illustrations of it.
, and the numerical tables showed this as well. [To download the original Mathematica notebook, click on the icon to the right. The "example" link shows the same information in a browser window.] The formal proof, the graph, and the numerical tables were all in front of the students at once -- I had to move between these various presentations of the same concept several times. Finally, one by one, the students’ faces signaled understanding. They had grasped the meaning of the formal mathematical proof, but only after they had seen the visual and numerical illustrations of it.
![]() After that point, I changed the construction of the remaining units. I had a careful presentation in the classroom of each new topic before we went to the lab. The lab then gave numerical and graphical support of the concept; the follow-up after the lab reinforced the connection between the concepts and the formalism. There were many "aha!" moments, in my office and in the classroom. One of the most successful labs illustrated the idea of uniform convergence, using the
After that point, I changed the construction of the remaining units. I had a careful presentation in the classroom of each new topic before we went to the lab. The lab then gave numerical and graphical support of the concept; the follow-up after the lab reinforced the connection between the concepts and the formalism. There were many "aha!" moments, in my office and in the classroom. One of the most successful labs illustrated the idea of uniform convergence, using the ![]() finally fit into the outline formed by the two curves
finally fit into the outline formed by the two curves ![]() and
and ![]() , for the interval
, for the interval ![]() .
.
In this real analysis class, students could see how the formalism of the text was the final step in the process -- when the ideas were put into the language of mathematics. They especially enjoyed their own successes in writing proofs and presenting them to their classmates. They finally understood that the purpose of the course was to make more precise and formal some deep mathematical concepts, and that we were trying to investigate these concepts in a variety of ways.
By the end of the semester, in a classroom discussion that was taped, students expressed a very positive attitude about the course and the laboratory experience. They felt that they had struggled with some highly abstract material, but the varied activities of the course helped them understand the concepts deeply. The technology was one component -- but clearly not the only one -- that helped them learn.What we all came to realize is that the use of technology in this course helps students bridge the huge gap between their very loose grasp of the concepts learned in beginning calculus and the highly formal and somewhat non-intuitive rigor of real analysis. My contribution to the multidisciplinary DePauw Faculty Instructional Technology Support program (FITS) was twofold: first, that the instructor cannot assume that techniques that work in one course will transfer to another course, and second, that the success of such a course can be enhanced by allowing the students to be part of the process.
Ellen J. Maycock, "Technology in the Upper-Level Curriculum - Real Analysis," Convergence (November 2004)




