- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Transport Equation and Directional Derivatives - Introduction
The transport equation is a partial differential equation of the form
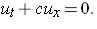 |
(1) |
Here, u is a function of two variables x and t, and the subscripts denote partial derivatives. We will assume that c is a fixed constant. Given an initial condition
 |
(2) |
we would like to find a function of two variables that satisfies both the transport equation (1) and the initial condition (2).
This equation can be used to model pollution (Lehn and Scherer , undated), dye dispersion (Roychoudhury , undated), or even traffic flow (Jungel , 2002), with u representing the density of the pollutant (or dye or traffic, respectively) at position x and time t. For a discussion of the physical model, see Knobel (2000). For a discussion of the more general transport equation and its solutions, see Cooper (1998). For discussion and simulation of more general conservation laws, including shock wave phenomena, see Sarra (2003).
Acknowledgment
Components for the applet are based on David Eck's Java Components for Mathematics at Hobart and William Smith Colleges.
About the author
Joan Remski is an Assistant Professor of Mathematics
at University of Michigan-Dearborn .
Copyright 2004 by Joan Remski
Published June, 2004
Joan Remski, "The Transport Equation and Directional Derivatives - Introduction," Convergence (August 2004)




