- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Tool Building: Web-based Linear Algebra Modules - Discussion of GridMaster
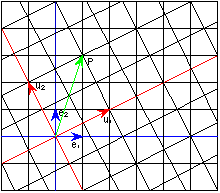
![]() In January of 2002, we discovered a paper entitled "Multigrid Graph Paper" (Bevis, 2002) that claimed multigrid paper (see Figure 1) would be helpful for students studying a variety of linear algebra concepts such as linear transformations, change of bases, and coordinate systems.
In January of 2002, we discovered a paper entitled "Multigrid Graph Paper" (Bevis, 2002) that claimed multigrid paper (see Figure 1) would be helpful for students studying a variety of linear algebra concepts such as linear transformations, change of bases, and coordinate systems.
|
|
Figure 1. Multigrid paper |
In Figure 1 we can see that vector P has coordinates [1,3] with respect to the natural basis {e1, e2}, but with respect to {u1, u2}, the vector P has coordinates [1,1].
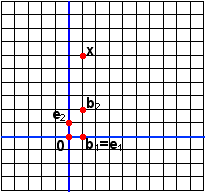
We saw the multigrid paper as a means of streamlining the Lay (2003) presentation of coordinate systems using two different graph papers. In particular, Lay (2003) described the use of two separate grids similar to those shown in Figures 2 and 3 when negotiating between two coordinate systems. For instance, the vector x has coordinates 1 and 6, typically expressed as ![]() with respect to the natural basis {e1, e2} (see Figure 2). In contrast, Figure 3 displays the vectors b1, b2 and x, but in reference to a grid defined by b1 and b2. The position of x has not moved, but
with respect to the natural basis {e1, e2} (see Figure 2). In contrast, Figure 3 displays the vectors b1, b2 and x, but in reference to a grid defined by b1 and b2. The position of x has not moved, but ![]() .
.
 |
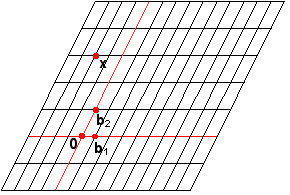 |
Figure 2. Standard graph paper |
Figure 3. B-graph paper |
After examining Bevis' article, which suggested overlaying multiple grids on a single sheet, we felt that static multigrid graph paper could be improved upon by using The Geometer's Sketchpad. The resultant web-based module, entitled GridMaster, permits students to model a portion of R2 and define vectors that coordinatize this vector space. Specifically, this first module was designed to help students recognize the meanings of different coordinate systems and change of bases, two topics identified as difficult for students to understand (Carlson, 1993).
In addition, we sought to address an observation of Hillel (2000) that some of the representations used in linear algebra can serve as obstacles to the development of student understanding. Hillel specifically identified that students have difficulty generalizing the notion of an n-tuple as no longer representing a single vector but a potential representation of any other vector. This is of significant importance when students have to work across different bases. This observation motivated us to look for different ways, other than the purely computational MATLAB interactions we had used before, to cause students to interact with multiple representations simultaneously.
Next ![]() or
or ![]() or
or ![]() page: 4. GridMaster Tool and Sample Activity
page: 4. GridMaster Tool and Sample Activity
David E. Meel and Thomas A. Hern, "Tool Building: Web-based Linear Algebra Modules - Discussion of GridMaster," Convergence (May 2005)