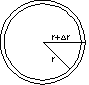- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Rethinking Pythagoras - 2. The Plane Truth
We begin our explorations in Euclidean geometry, the most familiar geometry to most of us. Euclidean geometry might best be explored via the wonderful Euclid's Elements [6], a reproduction of Euclid's own work, written in English, and published with an applet accompanying each theorem to aid in visualization. Wikipedia's Euclidean Geometry page [7] and Wolfram MathWorld's Euclidean Geometry page [8] are also good references.
Most students have seen the Pythagorean Theorem so many times that they have lost count. Many have seen at least two or three proofs of it as well, though most would be hard pressed to recall one, much less elucidate what, exactly, constitutes a proof. While dynamical software allows discovery of concepts for making conjectures, many students are more convinced by their "discoveries" via dynamic software than by mathematically rigorous proofs. We hope to use that surety students have with their own discoveries to convince them of the need for actual proof.
We first consider Figure 1b in the Euclidean plane. Although it is easy to evaluate the area of a circle using the well-known formula \(A=\pi r^2\) (where \(A\) represents the area and \(r\) the length of the radius of the circle, both as measured in Euclidean geometry), finding the formula in the first place requires some knowledge of calculus. (It is true that the formula was discovered long before calculus, but the methods involved used limits, a concept that is now taught as part of calculus.)
One such method is to cut the circle into evenly many pie sections, and rearrange the sections as shown in Figure 2. In Figure 2a, the circle has been cut into 4 pie sections, and in Figure 2b into 10. The idea is clear when viewed in the linked animation [9]. It can be seen that the resulting figure approaches a parallelogram (indeed, a rectangle) as the number of slices becomes large. The limiting rectangle has height \(r\) and width equal to half the circumference of the circle. Since the number \(\pi\) is often defined as the ratio of the circumference of a circle to its diameter, half the circumference is \(\pi r\). The area of the limiting rectangle, and thus the circle itself, must therefore be \(\pi r^2\).
Here we have assumed that \(C=2\pi r\). However, this is often used as the definition of the number \(\pi\). We refer to Playground Tutorial Video 3 for an exploration of the constancy of the circumference to radius ratio in Euclidean geometry.
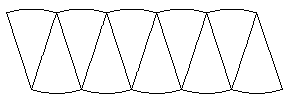
Figure 2b.
2.1 Using Differential Calculus
Another method might be to recognize that as the radius of the circle changes by a small amount, say \(\Delta r\), the area grows at approximately the circumference times \(\Delta r\), or \(\Delta A=2\pi r\Delta r\). (Note again the assumption that the circumference of a circle is \(2\pi r\).) The relationship \(\Delta A=2\pi r\Delta r\) is shown in Figure 3, where in Figure 3a, circles are shown with radius \(r\) and \(r+\Delta r\), in Figure 3b the strip between them is beginning to be "unrolled," and in Figure 3c it has been completely flattened, showing the approximate relationship. Moving to the limit, we obtain \(\frac{dA}{dr}=2\pi r\). Taking the antiderivative, we then obtain \(A=\pi r^2+K\), for some constant \(K\). Looking at the \(r=0\) case, we quickly see that \(K=0\), in other words, \(A=\pi r^2\).
Figure 3c.
Figure 3b.
2.2 Using Integral Calculus
A third method is to set up and evaluate a definite integral. In this case, we assume that the circle of radius \(r\) is centered at the origin, so that we are considering the curve \(x^2+y^2=r^2\). Solving for \(y\), we obtain \(y=\pm(r^2-x^2)^{1/2}\). We want to find the area under this curve, or twice the area under the top half, between \(x=-r\) and \(x=r\), in other words, \(A=2\int_{-r}^{r} (r^2-x^2)^{1/2} dx\). After making the trigonometric substitution \(x=r\sin \theta\), and a little simplifying, we obtain \(A=2r^2\int_{-\pi/2}^{\pi/2}\cos^2 \theta d \theta\). This can be evaluated quite simply, giving us the standard area formula \(A=\pi r^2\). We could also use an arclength integral to show that \(C=2\pi r\), or simply differentiate the area formula.
Alternately, we can use polar coordinates. In this case, we need to integrate \(A=\int_0^{2\pi} \frac12 r^2 d \theta\), which again gives us the standard area formula \(A=\pi r^2\).
2.3 The Pythagorean Theorem
Once we have agreed on an algebraic formula for the area of a circle, we can move to the Pythagorean Theorem. In Geometry Playground [1], we construct a right triangle with circles along each edge, as appears in Figure 1b.
To construct a right triangle, construct a segment, then a perpendicular through one of the endpoints. Construct a point on that perpendicular line, and then hide the line. Now it is possible to construct the two segments joining the point on the perpendicular to the endpoints of the original segment. It is straightforward to construct circles along each edge such as appear in Figure 1b.
For those who prefer to have a jump-start, you can open Geometry Playground with a pre-constructed Euclidean right triangle. Again, it is straightforward to construct circles along each edge.
Measuring the areas of the circles and exploring the relationships between those areas, hopefully the relationship \(\pi a^2+\pi b^2=\pi c^2\) will eventually stand out. Dividing by \(\pi\) yields the Pythagorean Theorem. Hurray! We have proven the Pythagorean Theorem! Or have we? Really, what we have done is discover that Geometry Playground seems to imply the Pythagorean Theorem, at least in the cases we have looked at so far. This is far from a proof! It is time to go exploring in a world closer to our own.
Daniel J. Heath (Pacific Lutheran University), "Rethinking Pythagoras - 2. The Plane Truth," Convergence (May 2011), DOI:10.4169/loci003568