- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Student Module for 'Thinking Outside the Box'
Introduction
Perhaps one of the deepest entrenched calculus problem is the canonical box problem that students encounter when discussing applied extrema problems. In fact, Friedlander and Wilker (1980) commented, ''This question must be answered nearly a million times a year by calculus students from every corner of the globe'' (p. 282). Without a doubt, almost every recently published calculus text contains a problem similar to the following:
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. Congruent squares are to be cut from its four corners. The resulting piece of cardboard is to be folded and its edges taped to form an open-topped box (see figure below). How should this be done to get a box of largest possible volume?

Figure 1: Canonical Box Problem
In particular, this problem (or some derivative of it) occurs in a classic text such as Thomas (1953), Granville and Smith (1911) and Todhunter (1855) as well as modern texts such as Stewart (2008), Larson, Hostetler and Edwards (2007) and Smith and Minton (2007). But, what about this problem makes it so common and prevalent to the calculus experience? This module allows you to take a closer look at this common box problem and then presents a better box problem more consistent with modern box building techniques.
So, if you really enjoy this original box problem, an applet, called OpenBox, has been developed for this problem. For this applet, the yellow points are moveable and control the size of the sheet of cardboard and the position of the cut. A dynamical graphic contained in a grey box shows the graph of the Volume to cut length (x) function. In addition, a dynamical picture of the open box is provided to illustrate how the changes in cut length impacts the configuration of the open box.
Click Here to open the Open Box Problem applet
Warning: The OpenBox applet is best viewed in 1024 x 768 resolution or greater and may take up to a minute to load.
However in the rest of this module, you will focus on a new box problem, tied much closer to reality. In particular, you will be engaged in exploring this improved box problem and its real-world context along with activities that blend hands-on and applet-based investigations with a strong dose of analysis that culminates in other possible extensions and investigations.
The New Box Problem
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. If six congruent cuts (denoted in black) are to be made into the cardboard and five folds (denoted by dotted lines) made to adjoin the cuts so that the resulting piece of cardboard is to be folded to form a closeable rectangular box (see figures below). How should this be done to get a box of largest possible volume?
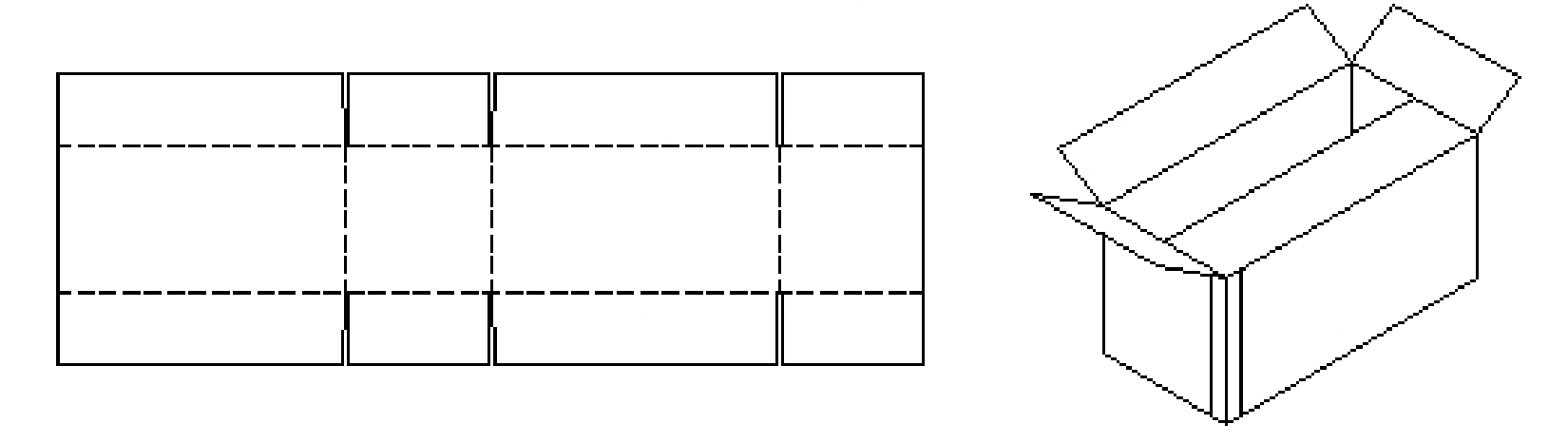
Figure 2: The box problem graphics
Before interacting with the Box problem applets and activities, you should first watch the video of such a box being manufactured and then take a rectangular piece of cardboard and attempt to physically build your own box using scissors and tape or at least find a RSC and dissect it. What did you notice from doing this activity?
Questions to be answered before moving on to the first Box problem applet and activity:
- What does a ''closeable rectangular box'' infer about the characteristics of the box?
- What impact does closeable mean with respect to the length of at least a pair of the flaps?
- Should the flaps overlap? and
- If they do overlap, is that the best use of the cardboard?
David Meel and Thomas Hern, "Student Module for 'Thinking Outside the Box'," Convergence (August 2009)




