- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - February 2016
I enjoy when mathematics is motivated or inspired from a real-life situation. The first two articles are prime examples. In the first, Jessica Sklar and Tom Edgar were motivated by unusual wiring in a home that leads to analysis of the Lights Out game. The second article by Franklin Mendivil and Jeff Hooper considers permutations related to the transpose of a matrix, motivated from a data storage perspective.
Elsewhere in the issue, Elizabeth Wilcox channels Lewis Carroll to explore the Chermak-Delgado lattice and Burkard Polster and Marty Ross consider Pythagorean-like visual proofs. Besides an interview with woodcarver Bjarne Jespersen, there are also some proof without words, the Reviews and Problems sections, and the solutions to the 76th Annual Putnam Competition.
—Michael A. Jones, Editor
JOURNAL SUBSCRIBERS AND MAA MEMBERS:
To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.
Vol. 89, No. 1, pp 1 – 79
Articles
A Confused Electrician Uses Smith Normal Form
Tom Edgar and Jessica K. Sklar
In this paper we define “confused electrician games,” which generalize “Lights Out,” a game popular in mathematical literature. In addition to “Lights Out,” many more recent computer game puzzles can be modeled as confused electrician games.We provide examples of this, and explain how to solve such games using the Smith normal form of a matrix. We note that in many cases, this method is very efficient compared to another, more obvious, method.
To purchase from JSTOR: 10.4169/math.mag.89.1.3
Proof Without Words: Perfect Numbers and Sums of Odd Cubes
Roger B. Nelsen
We show wordlessly that every even perfect number greater than six is a sum of consecutive odd cubes.
To purchase from JSTOR: 10.4169/math.mag.89.1.14
Transposition as a Permutation: A Tale of Group Actions and Modular Arithmetic
Jeff Hooper and Franklin Mendivil
Converting a matrix from row-order storage to column-order storage involves permuting the entries of the matrix. How can we determine this permutation given only the size of the matrix? Unexpectedly, the solution to this question involves the use of elementary group theory and number theory. This includes the Chinese remainder theorem, finding multiplicative generators modulo pn for prime p, and using these to find orbit generators for a group action, a subgroup of acting on all of ℤN.
To purchase from JSTOR: 10.4169/math.mag.89.1.16
Proof Without Words: Sum of Triangular Numbers
Ángel Plaza
The triangular numbers are given by the following explicit formulas: Tn = 1 + 2 + ⋯ n =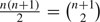 . Here it is proved visually that
. Here it is proved visually that  .
.
To purchase from JSTOR: 10.4169/math.mag.89.1.36
Exploring the Chermak-Delgado Lattice
Elizabeth Wilcox
Need a project to satisfy your craving for abstract algebra? Or do you have a student nosing around your office looking for a project? The Chermak–Delgado lattice is a sublattice of the subgroup lattice of a finite group. The details of its definition don′t require advanced group theory, though working with this lattice can send one on a journey through deeper, more advanced techniques. This makes the Chermak–Delgado lattice the perfect starting point for an undergraduate project after an abstract algebra class. This article guides the curious reader through a series of exercises about the Chermak–Delgado lattice to provide preparation and fuel interest, before posing several open-ended questions for investigation.
To purchase from JSTOR: 10.4169/math.mag.89.1.38
Proof Without Words: The Sum 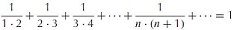 and Its Partial Sums
and Its Partial Sums
Óscar Ciaurri
We provide a visual proof of the identity 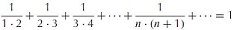 including its partial sums.
including its partial sums.
To purchase from JSTOR: 10.4169/math.mag.89.1.45
One-Glance(ish) Proofs of Pythagoras′ Theorem for 60-Degree and 120-Degree Triangles
Burkard Polster and Marty Ross
In this article we present some elementary proofs of the 60-degree and 120-degree counterparts of Pythagoras′ theorem that mimic the two (most) famous one-glance proofs of Pythagoras′ theorem.
To purchase from JSTOR: 10.4169/math.mag.89.1.47
Bjarne Jespersen: The Magic Woodcarver*
Amy L. Reimann and David A. Reimann
To purchase from JSTOR: 10.4169/math.mag.89.1.55
Problems and Solutions
Proposals, 1986-1990
Quickies, 1057-1058
Solutions, 1956-1960
Answers, 1057-1058
To purchase from JSTOR: 10.4169/math.mag.89.1.58
Reviews
Moral hazard; recreational mathematics; Tower of Hanoi; crime in L.A.
To purchase from JSTOR: 10.4169/math.mag.89.1.67
News and Letters
76th Annual William Lowell Putnam Mathematical Competition
To purchase from JSTOR: 10.4169/math.mag.89.1.69





