1. How Seashells Grow
You have certainly noticed that the shell of an immature mollusk often resembles fully grown shells of the same species but in miniature.
Each one is an exact model, to scale, of the other.
Seashells, with their auto-similar shape, may be represented by a three-dimensional surface,
generated by a simple equation, with some free parameters. Amazingly, in spite of the simplicity of that equation,
it is possible to generate a great variety of seashell types. Which ones?
All of them! (with a very few exceptions: some live and fossil species of Vermicularia
and fossil ammonites of the class of Didymoceras.)
This shows how many of the forms that appear in nature
are simple consequences of the
application of three-dimensional geometry
to the basic rules of growth.
The mollusk does not enlarge its shell in a uniform way: it only adds material in one of the edges of the shell (the open or "growth" ending) and makes it in such a way that the new shell is always an exact model, to scale, of the smaller shell.


These constraints have a mathematical consequence:
almost every shell follows a growth rule based on an equiangular spiral (Section 1.1):

This was first noted by Christopher Wren in the 17th century. A clear mathematical model of shell growth based on equiangular spirals was given
by Henry Moseley in 1838, and the model used here is a direct extension of his (M. B. Cortie [1]). Careful studies from the mid-1800s to mid-1900s validated Moseley's basic model
for a wide variety of shells.
The surface of a shell is a three-dimensional surface that may be regarded as the result of a deplacement of a curve C (the generating curve, usually an ellipse) along an helico-spiral H (the structural curve); the width of the curve C increases as far as it moves along H:
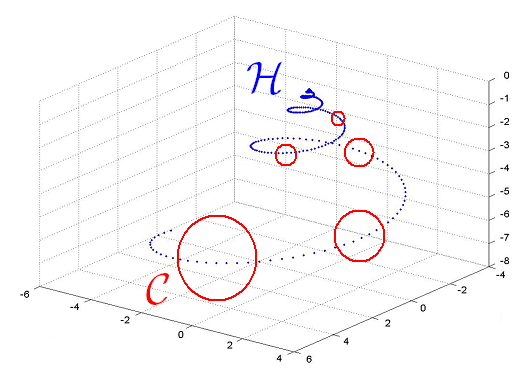


which is generated by a triangular curve.
Why is H an helico-spiral? Basically because the mollusk does not enlarge its shell in a uniform manner:
it secretes shell material faster on one side than the other of the open edge of the shell. A two-dimensional version of this
phenomenon may be observed
in the growth of animal horns. Essentially it is a three-dimensional version of this phenomenon that
yields the spiral structures of the shells of mollusks.
See this for a more precise explanation.
The following examples show three of the cases that may occur. The first example is typical of the nautilus shell, the second one of a cone and the third one of the clam of a bivalve. In each case the new shell material is progressively added in the aperture of the shell.
The effects of varying some of the growth parameters of seashells may be observed in the following pictures. They show that, with the same model, every type of seashell shape may be produced.
Varying the overall factor by which the size increases in the course of each revolution (by increasing order, from left to right):

Varying the relative amount by which the opening is displaced downward at each revolution (by increasing order, from left to right):

Varying the size of the opening relative to the overall size of the shell (by increasing order, from left to right; shells like the first three, where sucessive
whorls do not touch, appear to be significantly less common than others, perhaps because they have lower mechanical rigidity; they occur mostly as internal rather
than external shells):

Varying the elongation of the opening (by increasing order, from left to right):

Variying the orientation of elongation in the opening (from vertical orientation to the horizontal orientation, from left to right):

