3. The complete model
In case we want to add nodules, bumps and spikes
to the shell, it suffices to include some additional parameters [1], illustrated in the following
picture:

- W1: width of nodule along the generating curve (in s-direction)
- W2: width of nodule along the helico-spiral (in
 -direction)
-direction) - L: height of nodule at
 =0
=0 - P: position of nodule in terms of the angle s
- N: number of nodules per whorl.
From [M. B. Cortie, Modelling the surface bumps and spikes of molluscan shells, in: Proceedings of the First International Conchology Conference (Ed. C.R. Illert), Hadronic Press, Palm Harbor, 1995, pp. 46-65], if a surface sculpture term is superimposed in the generating ellipse C, it suffices to replace the equation re(s) of C
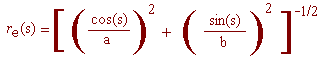




Based on the above description, the parametric equations of the shell depend on 14 parameters
-
D, A,
 ,
,  ,
, 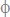 ,
,  ,
,
 , a, b, L, P, W1, W2, N
, a, b, L, P, W1, W2, NVarying parameters L, P, W1, W2 and N changes significantly the shape of the shell. In order to understand better the effect of these new parameters in the shape of the shell, see the following interactive applets in the web page of the Portuguese project Atractor (of popularization of mathematics) [10]:
- Effect of the variation of L, P and W1 along the generating curve.
- Effect of the variation of L, P and W2 along the helico-spiral.
- Effect on the shell shape of the variation of: parameter L, parameter P, parameter W1, parameter W2, parameter N.
Finally, the dimensions:
 min,
min,  max: min and max values of
max: min and max values of 
- smin, smax: min and max values of s

The parameters  d and sd determine the resolution of the generated shell (for
example, if the shell contains nodules that are thin and long we have to use very small
d and sd determine the resolution of the generated shell (for
example, if the shell contains nodules that are thin and long we have to use very small
 d and sd values in order to shape the nodules).
d and sd values in order to shape the nodules).
Implementation of the model
The implementation of this model with Mathematica can be effected in the following way
(since the XYZ referential we use in our model has opposite orientation to the one used by Mathematica,
we change the sign in coordinate y):
l[n_][theta_] = (2Pi/n)((n theta/2Pi) - IntegerPart[n theta/2Pi]);
k[a_,b_,ll_,p_,w1_,w2_,n_][s_,theta_] = If[w1=0||w2=0||n=0,0, ll Exp[-(2(s-p)/w1)^2-(2l[n][theta]/w2)^2]];
h[a_,b_,ll_,p_,w1_,w2_,n_][s_,theta_] = (1/(Sqrt[(Cos[s]/a)^2+(Sin[s]/b)^2])) + k[a_,b_,ll_,p_,w1_,w2_,n_][s_,theta_];
x[d_,aa_,beta_,phi_,omega_,mu_,alpha_,a_,b_,ll_,p_,w1_,w2_,n_][theta_,s_] =
d(aa Sin[beta] Cos[theta] + h[a,b,ll,p,w1,w2,n][s,theta]
(Cos[s+phi] Cos[theta+omega] - Sin[mu] Sin[s+phi] Sin[theta+omega])) Exp[theta Cot[alpha]];
y[aa_,beta_,phi_,omega_,mu_,alpha_,a_,b_,ll_,p_,w1_,w2_,n_][theta_,s_] =
(-aa Sin[beta] Sin[theta] - h[a,b,ll,p,w1,w2,n][s,theta]
(Cos[s+phi] Sin[theta+omega] + Sin[mu] Sin[s+phi] Cos[theta+omega] ))Exp[theta Cot[alpha]];
z[aa_,beta_,phi_,mu_,alpha_,a_,b_,ll_,p_,w1_,w2_,n_][theta_,s_] =
(-aa Cos[beta] + h[a,b,ll,p,w1,w2,n][s,theta] Sin[s+phi] Cos[mu]) Exp[theta Cot[alpha]];
%EXAMPLE: BOAT EAR MOON SHELL
With[{d=1,aa=25,beta=42Degree,phi=70Degree,omega=30Degree,mu=10Degree,alpha=83Degree,a=12,b=20,ll=0,p=0,w1=0,w2=0,n=0},
ParametricPlot3D[{x[d,aa,beta,phi,omega,mu,alpha,a,b,ll,p,w1,w2,n][theta,s],
y[aa,beta,phi,omega,mu,alpha,a,b,ll,p,w1,w2,n][theta,s]
z[aa,beta,phi,mu,alpha,a,b,ll,p,w1,w2,n][theta,s]},
{theta, -4Pi, 4Pi}, {s, 0 Degree, 360 Degree},
Boxed -> False, Axes -> False, PlotPoints -> {100,20}, PlotRange -> All, ViewPoint -> {-1,-3,0.5}]]

