Like friezes, wallpaper patterns have rotocenters about which a basic unit can be rotated. The smallest angle that a fundamental domain can be rotated determines the order of the rotocenter of a wallpaper pattern. For example, if a fundamental domain can be rotated by a 1/2-turn, the pattern is of order 2. The only possible orders for the rotocenters of wallpaper patterns are 2, 3, 4, and 6.

In addition to rotation, wallpaper patterns have reflections and glide reflections. These symmetries rely on mirror lines in the plane of the pattern. Unlike in friezes, it is possible to have glide lines that are not mirror lines.

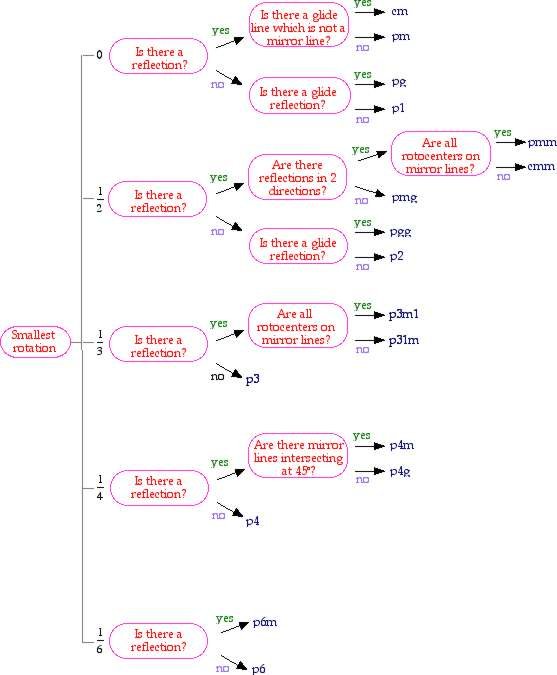
Like frieze patterns, wallpaper patterns can be divided into classifications using a simple flow chart (see the figure below). In 1891 E. S. Fedorov proved that there are exactly 17 possible wallpaper patterns.

Click here to see examples of the 17 wallpatterns.