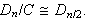Conjectures
December 2001
- (BJT conjecture) Every subgroup

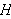 of a finite group
of a finite group 
 which has index 2 in
which has index 2 in 
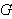 is a normal subgroup of
is a normal subgroup of 
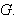
- (CEK corollary) The subgroup of all rotations of

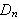 is a normal subgroup of
is a normal subgroup of 
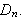
-
(9-conjecture) The commutator subgroup of any group is normal.
-
(7-conjecture) The center of any group is normal.
-
(6-conjecture) Let

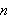 be odd, and let
be odd, and let 
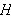 be the commutator subgroup of
be the commutator subgroup of 
 Then
Then 

-
(DJKT conjecture) Let

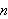 be even and let
be even and let 
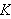 be the commutator subgroup of
be the commutator subgroup of 
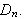 Then
Then 
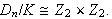
- (Kevin's conjecture) Let

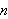 be even and let
be even and let 
 be the subgroup of
be the subgroup of 
 consisting of the identity and the 180
consisting of the identity and the 180
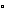 rotation. Then
rotation. Then 
 is normal in
is normal in 
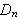 and
and 
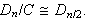
Students who contributed the conjectures:
-
BJT: Brian, Jon, Tege
-
CEK: Charlie, Erika, Kevin
-
DJKT: Dale, Jon, Kevin, Tege
-
9: Brian, Charlie, Dale, Jean-Marc, Jon, Kevin, Krista, Otto, Tege
-
7: Brian, Charlie, Dale, Jean-Marc, Kevin, Krista, Otto
-
6: Erica, Jon, Kevin, Krista, Otto, Tege
This document created by Scientific WorkPlace 4.0.

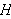 of a finite group
of a finite group 
 which has index 2 in
which has index 2 in 
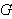 is a normal subgroup of
is a normal subgroup of 
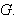

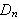 is a normal subgroup of
is a normal subgroup of 
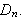

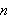 be odd, and let
be odd, and let 
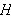 be the commutator subgroup of
be the commutator subgroup of 
 Then
Then 


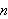 be even and let
be even and let 
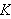 be the commutator subgroup of
be the commutator subgroup of 
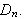 Then
Then 
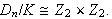

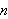 be even and let
be even and let 
 be the subgroup of
be the subgroup of 
 consisting of the identity and the 180
consisting of the identity and the 180
 rotation. Then
rotation. Then 
 is normal in
is normal in 
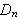 and
and