Mathematical Treasures of Japan in the Edo Period
Introduction
This article was inspired by the 2011 exhibit and website Japanese Mathematics in the Edo Period, produced by the National Diet Library of Japan. The Edo Period of Japanese history is generally considered to span the years 1603-1867 CE. The National Diet Library exhibit focused on Wasan, which Sato Ken'ichi and Orita Hiroharu, in their Introduction to the online version of the exhibit, defined as "the indigenous mathematics of Japan" and as "the mathematics that developed in Japan before the Edo period, independently from Western mathematics." This is not to say that indigenous mathematical development ceased during the Edo period; in fact, "Wasan was at its peak" during this period, with many scholars making great progress and many books produced. Nor does the exhibit ignore the influence of Western scholarship during the period: in Chapter 1. Early Edo Period, the exhibit authors wrote that the gradual incursion of Western mathematics resulted in Wasan being "replaced by its Western counterpart immediately after the start of the Meiji era" (1868-1912).
We begin with sangi, or counting, rods first used in China and, subsequently, in Korea and Japan.
Sangi Rods and Computing Surface
Sangi rods and a computing surface, like those shown below, were used for calculations in Edo Period Japan.

The Japanese system of computing using sangi rods was adopted from the Chinese. The Chinese rods were called saunzi. The characters across the top row of the inscription designate number groupings. For the rod configuration shown, the row entries reading right to left designate units, tens, and hundreds. Thus, the rod configurations appear to be addends for a sum. Reading down the columns: “23 + 144 + 48 + 1.”
To view a set of counting rods from Korea, see Mathematical Treasures – Korean sangi rods, here in Convergence.
The image above is presented through the kind cooperation of the National Diet Library, Japan, and is used with permission. It was obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period.
See the list below for additional information about and images of mathematical texts and tools from the Japanese Edo Period, presented as "pages" in this Convergence digital "book." For texts from other institutions and cultures, see our Index of Mathematical Treasures; to find other tools and instruments, check our Index of Mathematical Objects.
Mathematical Treasures of Japan in the Edo Period: Arithmetic on the Japanese Abacus
The Japanese adopted their bead abacus, the soroban, from the Chinese suanpan which was introduced into Japan in the 14th century. The mathematician Yoshida Mitsuyoshi (1598-1673) published Shinpen jinkoki (1627) as a manual to teach basic operations using the soroban. Many later editions were published. The following images are from such a later edition. The cover bears an interesting configuration of numerals:

Instructions on using a soroban are accompanied by illustrations:

For more explicit instructions about how to use the soroban, see the Convergence article, Elementary Soroban Arithmetic Techniques in Edo Period Japan, by Rosalie Joan Hosking, Tsukane Ogawa, and Mitsuo Morimoto.
On the pages below, two situational problems are given: one involving a river, the other the sharing of an inheritance. The “inheritance problem” on the right is an example of the Josephus Problem in combinatorics: people or objects are arranged in a circle so that in an elimination process that traverses the circular arrangement several times, certain people or objects remain. The scheme of elimination should be to the advantage of the instigator who has arranged the scheme to his or her benefit.
In this particular case, a mother arranges her children, some of whom are her birth children and others of whom are her step-children, in the circle, scheming that in the elimination process her birth children will remain and obtain an available inheritance. However, she has figured wrong and her preferred children are eliminated. A mathematical problem with a moral!

Below: A problem situation is given where two gardeners wish to determine the height of a tree. They use different methods: one employing a plumb-bob, the other a staff.

Some final problems involve geometric objects in their problem situations:


See images from another copy of Shinpen jinkoki here in Convergence and in the exhibit described below.
These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Arithmetic
Shinpen jinkoki (1689) is a basic mathematics text originally written by Yoshida Mitsuyoshi (1598-1673) in 1627. The title page bears his seal:
Work using elementary operations is explained and illustrated with examples. A reader familiar with traditional Chinese/Japanese numerical notation can attempt to decipher the problem contents:

Area computation for common geometric shapes is taught:

See images from another copy of Shinpen jinkoki here in Convergence and in the exhibit described below.
The images above are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Arithmetic and Algebra
Shinpen sangaku keimo (1690) is a reprinting of the Chinese work, Suanxue qimeng (1299), by Zhu Shijie (c.1260-1320). The Japanese mathematician Takebe Katahiro (1664-1739) added a commentary. The work teaches basic arithmetic operations and Chinese algebraic solution methods, or tian yuan shu, for solving polynomial equations of higher degree. The title page is shown below.

Problem calculations and explanations are carried out using rod numerals:


These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Determinants
Seki Takakazu (c.1642-1708), the leading mathematician of the Edo Period (1603-1867) in Japan, is credited with developing a theory of mathematical determinants for solving systems of linear equations. Kaifuku dai no ho is a page of an existing manuscript illustrating Takakazu’s methods of setting up and working with determinants.

These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Circles and Spheres
Kigenkai is a mathematical investigation on circles and spheres. In particular, the volume of a sphere is derived, a value for \(\pi\) estimated, and arc length discussed. The text has been modified and amended by many generations of Japanese scholars, but it is often attributed to Seki Takakazu (also known as Seki Kowa, c.1642-1708), the leading mathematician of the Edo Period (1603-1867). The title page begins the text:

The volume of a sphere is obtained through “slicing”:

The area of a circle is obtained through a process of geometric iteration from which a value for \(\pi\) is obtained. This method is the same as that used by the Chinese mathematician Liu Hui several centuries prior:

For more of the mathematics of Seki Takakazu (also known as Seki Kowa), see Mathematical Treasures - Seki Kowa's Essentials of Mathematics, by Frank J. Swetz and Victor J. Katz.
The images above are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Surveying
Kiku yoho kuden shiroku is a surveying manual originating with the mathematician Shimizu Sadanori (1645-1717), then passed down and modified by successive scholars. The edition examined here is from the later 18th century. (The Edo Period spans the years 1603-1867.) The title page of Kiku yoho kuden shiroku contains the author’s seals.

The usual types of problems of determining the height of a distant inaccessible tower are considered.

Determining a distant height using a mathematical measuring instrument:

These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Napier's Rods for Japanese Samurai
Chusan shiki was written by the mathematician Arisawa Munesada (1689-1752). It is a book about the concept and use of Napier’s rods. This calculating device was invented in Europe and transmitted to China, from where it found its way into Japan. Munesada believed it was undignified and dishonorable for samurai to do calculations on a soroban, an instrument of merchants, and that they would be better served using the foreign Napier’s rods. Here is the title page:

A set of rods is illustrated on the left-hand page. The form of these rods is different in appearance than the Napier’s rods used in Europe. The Chinese modified the rods and the Japanese copied the Chinese version.

For more information about Napier rods or bones, see:
- John Napier: His Life, His Logs, and His Bones – Napier's Bones, by Michael J. Caulfield
- Mathematical Treasure: 17th Century Napier Rods, by Frank J. Swetz
The images above are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: The Chinese Nine Chapters in Japan
Sankei kyusho is a book of unknown authorship and date that is organized like and obviously influenced by the Chinese mathematical classic, Jiuzhang suanshu (The Nine Chapters on the Mathematical Art). In Sankei kyusho, the Japanese word kyusho means "nine chapters." The book concerns various practical mathematical applications. The opening page immediately focuses on solving problems.

Different geometrical situations involving measurement and calculation are considered.


For more information about the Jiuzhang suanshu (The Nine Chapters on the Mathematical Art), see:
- Mathematical Treasures - Jiuzhang suanshu, by Frank J. Swetz and Victor J. Katz
- Illustrating The Nine Chapters on the Mathematical Art: Their Use in a College Mathematics Classroom, by Joel Haack
These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Geometry
Shoho kongen is a geometry text focusing on obtaining the volumes of various polyhedra. It is assumed to have been compiled by the mathematician Matsunaga Yoshisuke (1692-1774) and employs dissection techniques to derive formulae for volumes. Instruction begins on the title page.

A convex polyhedron is subjected to several dissections.

The tetrahedron is examined in detail.

The frustum of a square pyramid is subjecting to “cutting”. The ancient Egyptians used similar methods in studying the properties of pyramids.
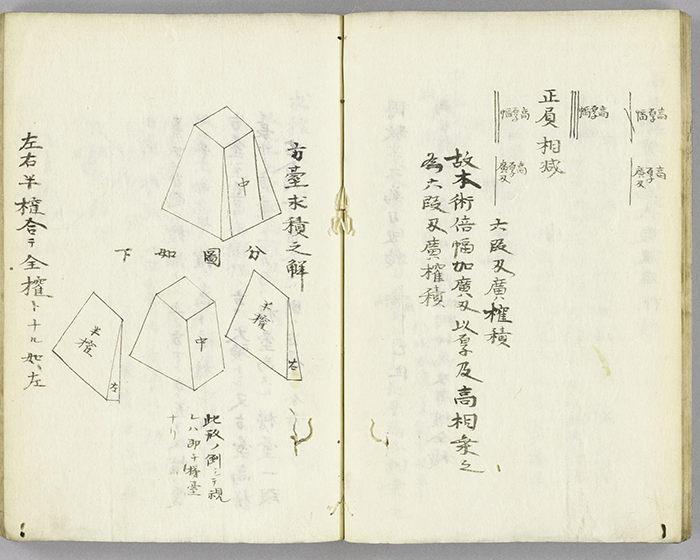
An example of “cutting corners”:

These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Practical Mathematics
Sanpo dojimon (Questions Children Ask About Mathematics, 1784) was a collection of problems concerning topics such as weights and measures, simple surveying, and the use of mathematical instruments. It is considered a Japanese classic of pedagogy of mathematics. The work's author was Murai Chuzen. A frontispiece depicts children asking their elders a question concerning mathematics, perhaps the distance to the sun, a question with which Chinese mathematicians grappled a millennium previous.
A scene of kite flying warrants the question, “How high is the kite?”

A variety of geometric situations involving inscribed configurations allows for a family of questions.

The illustration below demonstrates a simple technique for determining distance. Can you figure it out?

Two commoners have brought their feudal lord three baskets full of some commodity. Perhaps they are paying their required tribute (taxes) and there is a question concerning the capacities or weights of their contribution.

An illustration of a Japanese theodolite of this period accompanied by instruction as to its use:

The illustration shows the employ of a theodolite in taking a downward sighting.

These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.
Mathematical Treasures of Japan in the Edo Period: Circle Packing
Gomei sanpo (1826) was a collection of sangaku problems attributed to the mathematician Iesaki Yoshiyuki and assembled by publisher Osakaya Mokichi. This is the title page of the book.

Imaginative problem situations involving fitting circles into fans, i.e. circle-packing in fan-shaped regions:
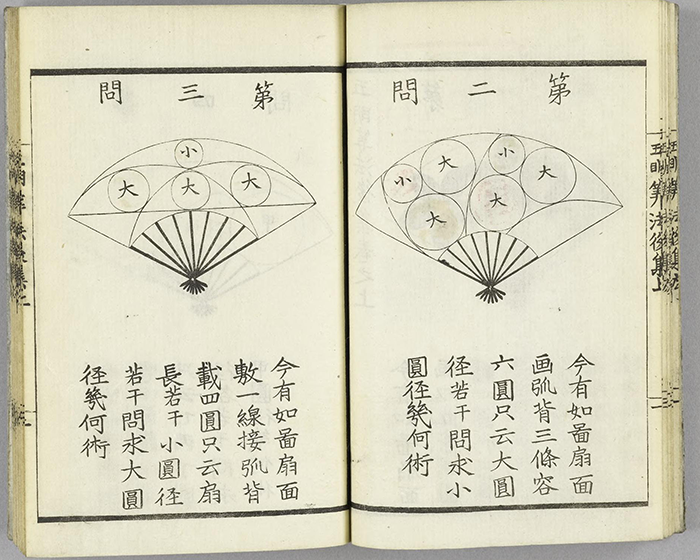
More typical problems involving circle packing and stacking:
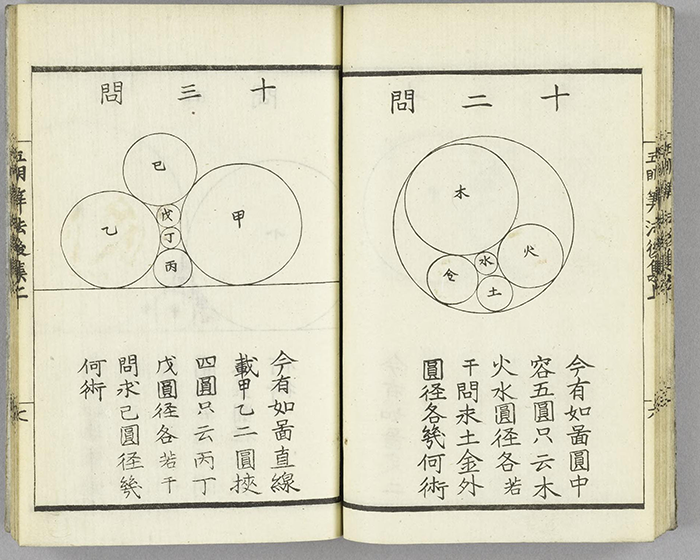
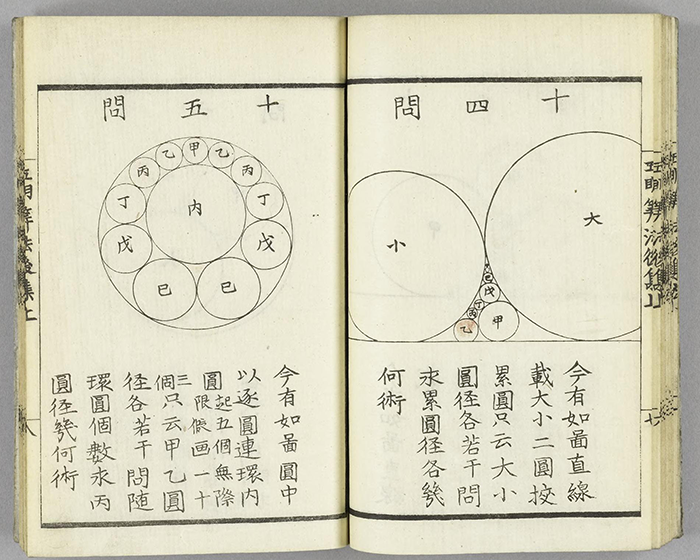
For another set of sangaku problems, see Mathematical Treasure: Japanese Temple Mathematics, by Frank J. Swetz, here in Convergence.
These images are presented through the kind cooperation of the National Diet Library, Japan, and are used with permission. They were obtained from the library’s digital gallery exhibit, Japanese Mathematics in the Edo Period, where a complete examination and viewing of the item presented above can be found.