Written by Abraham de Moivre (1667–1754), The Doctrine of Chances: A Method of Calculating the Probabilities of Events in Play was an early work in probability theory. It first appeared in Latin in 1711, with the first English edition published in 1718. Below is the title page of the 1738 English 2nd edition, “fuller, clearer, and more correct than the first.”

Next is an image of page 1 with the statement, “Wherefore, if we constitute a Fraction whereof the Numerator be the number of Chances whereby an Event happen, and the Denominator the number of all Chances whereby it may either happen or fail, that Fraction will be a proper designation of the Probability of happening.”

The next two images show some sample problems from the book. First is the solution to the problem “to find the Probability of throwing an Ace in two throws” on page 9, followed by a problem about three “Gamesters” on page 43.

Page 211 below contains a notation different from what is used today for \( (a + b)^2 \) and then the start of a section about annuities.

Images from a copy of the 1756 4th edition of The Doctrine of Chances, in which the normal distribution first appears, can also be found in Convergence.

A complete digital scan of the 1738 2nd edition of The Doctrine of Chances is available in the Linda Hall Library Digital Collections. The call number is QA273 .M63 1738.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

Renaissance man Gerolamo Cardano was a physician, mathematician, gambler, and writer. Cardano’s Ars Magna, published in 1545, is often considered the start of a comprehensive theory for solving algebraic equations. It was actually the tenth in a series of volumes Cardano wrote for a work he called Opus Perfectum, or The Perfect Work. Here is the title page:

Although he didn’t claim to be the first to come up with the techniques in the Ars Magna, Cardano was the first to publish a compilation of the known methods for solving polynomial equations up through degree four. In fact, there are places in the book where he gave credit to the originator of a particular method (e.g., Tartaglia). The page below (folio 29 verso) shows the start of Chapter XI, About the Cube and First Power Equal to a Number. The first paragraph, as translated by T. Richard Witmer, reads, “Scipio Ferro of Bologna well-nigh 30 years ago discovered this rule and handed it on to Antonio Maria Fior of Venice, whose contest with Niccolo Tartaglia of Brescia gave Niccolo occasion to discover it. He [Tartaglia] gave it to me in response to my entreaties, though withholding the demonstration. Armed with this assistance, I sought out its demonstration in [various] forms. This was very difficult. My version follows.”

Cardano did not write the general form for a quadratic equation as we do, namely \[ax^2 + bx + c = 0\] but instead only allowed positive coefficients and solutions. Thus, it took four different cases to include all possible quadratic equations. Three of the cases are #1–3 in the table below from Chapter II, About the Total Number of Rules. In English, these three cases are a number equal to a square and a linear term, a number and a linear term equal to a square, and a number and a square equal to a linear term. The case of a number equal to a square term was mentioned on the previous page. A possible activity in a high school or college algebra class would be to have students write these cases in modern notation and investigate why Cardano had these, and only these, four cases for quadratic equations.

Using his techniques, Cardano encountered a square root of a negative integer while solving a certain quadratic equation. Specifically, the problem was to find two numbers whose sum is 10 and product 40. The corresponding quadratic equation in modern notation is \[x^2 - 10x + 40 = 0\] For Cardano, this problem would have the form of a number and a square equal to a linear term. In his explanation, Cardano, writing in Latin dismissis incruciationibus, ignored the fact that there are negative radicands in the resulting two numbers, and he proceeded to show that the product of the two numbers, namely \[5 + \sqrt{-15}\] and \[5 - \sqrt{-15}\] was indeed 40. The phrase “dismissis incruciationibus” has been translated in different ways. In the Witmer translation (p. 219), it is “putting aside mental tortures” with an alternative translation of “the cross-multiples having canceled out” in a footnote, while Vera Sanford translated it as “the imaginary part being lost” (Smith, p. 202). The image (folio 66) below shows the corresponding page from Ars Magna.

More on Cardano’s methods for solving cubic and quartic equations can be found in the Convergence articles “Solving the Cubic with Cardano” and “A Modern Vision of the Work of Cardano and Ferrari on Quartics”.

For another image of the title page of Cardano’s Ars Magna, visit the page “Mathematical Treasures - Ars Magna Title Page” by Frank J. Swetz and Victor J. Katz in Convergence.

A complete digital scan of Ars Magna, call number QA35.C35 1545, can be found at https://catalog.lindahall.org/discovery/delivery/01LINDAHALL_INST:LHL/1286504780005961.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Branson, William B. "Solving the Cubic with Cardano." Convergence (September 2013). http://www.maa.org/press/periodicals/convergence/solving-the-cubic-with-cardano.

Helfgott, Harald, and Michel Helfgott. "A Modern Vision of the Work of Cardano and Ferrari on Quartics." Convergence (February 2010), DOI:10.4169/loci003312. http://www.maa.org/press/periodicals/convergence/a-modern-vision-of-the-work-of-cardano-and-ferrari-on-quartics-introduction.

O'Connor, J. J., and E. F. Robertson. “Girolamo Cardano.” MacTutor History of Mathematics archive. http://www-history.mcs.st-and.ac.uk/Biographies/Cardan.html.

Smith, David Eugene. A Source Book in Mathematics. Dover, 1959.

Swetz, Frank J., and Victor J. Katz. “Mathematical Treasures – Ars Magna Title Page.” Convergence (January 2011). http://www.maa.org/press/periodicals/convergence/mathematical-treasures-ars-magna-title-page.

Witmer, T. Richard, trans. Ars Magna or the Rules of Algebra. MIT Press, 1968. Reprint, Dover, 1993.

Index to Mathematical Treasures

The early 17^th-century Italian mathematician and disciple of Galileo, Bonaventura Cavalieri, developed a method of indivisibles for finding areas and volumes as a pre-cursor to the definite integral. He was a member of the Jesuati religious order (not to be confused with the Jesuits) and a mathematics professor at the University of Bologna for almost 20 years. According to Howard Eves, who considered the publication of Cavalieri’s Geometria indivisibilibus one of the “Great Moments in Mathematics,” “Cavalieri was one of the most influential mathematicians of his time, and the author of a number of works on trigonometry, geometry, optics, astronomy, and astrology." He was among the first to recognize the great value of logarithms and was largely responsible for their early introduction into Italy. But his greatest contribution to mathematics was a treatise, Geometria indivisibilibus, published in its first form in 1635, devoted to the pre-calculus method of indivisibles. The image below is the title page of this work, Geometria indivisibilibus continuorum nova quadam ratione promota (Geometry by indivisibles of the continua advanced by a new method).

The work is divided into seven books (libri). The next images show the beginning pages for each of the seven sections.

Book I: Book II:

Book III: Book IV: 

Book V: Book VI: 

Book VII: 

Below is proposition 3 of Book I (p. 21), which shows by construction that if a sphere is circumscribed by an arbitrary parallelogram, then opposite sides will be parallel.

The basis for Cavalieri’s determination of areas and volumes, now known as Cavalieri’s Principle, is given as Theorem 1 of Book 7, pictured below.

A complete digital scan of the Latin 1635 edition of Cavalieri’s Geometria indivisibilibus is available in the Linda Hall Library Digital Collections. The call number is QA33 .C359 1635. 

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Carruccio, Ettore. “Cavalieri, Bonaventura.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, iv:149–153. New York: Scribner, 1972.

Eves, Howard. Great Moments in Mathematics Before 1650. Mathematical Association of America, 1983, pp. 206–214.

O'Connor, J. J., and E. F. Robertson. “Bonaventura Francesco Cavalieri.” MacTutor History of Mathematics archive. http://www-history.mcs.st-and.ac.uk/history/Biographies/Cavalieri.html.

Index to Mathematical Treasures

The first printed Arabic version of Euclid’s Elements was in 1594 by the Medicean Press in Rome. It was based on an earlier 1260 manuscript by Nasīr al-dīn al-Tūsī, a well-known and influential Persian mathematician and astronomer. The copy at the Linda Hall Library of Science, Engineering & Technology is interesting since it was never bound. It is possible for readers to see what a book purchased in the 16th century directly from the publisher would have looked with its folded, unstitched, and uncut sheets.

For more on al-Tusi’s commentary of Euclid’s Elements, visit “Nasir al-din al-Tusi's Commentary on Euclid's Elements” by Frank J. Swetz and Victor J. Katz in Convergence.

The call number for this work is QA31.E86 1594. A complete digital scan is available in the Linda Hall Library Digital Collections.

Images in this article were taken by the author at the Linda Hall Library of Science, Engineering & Technology and are used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Swetz, Frank J., and Victor J. Katz. "Mathematical Treasures - Nasir al-din al-Tusi's Commentary on Euclid's Elements." Convergence (January 2011). http://www.maa.org/press/periodicals/convergence/mathematical-treasures-nasir-al-din-al-tusis-commentary-on-euclids-elements.

O'Connor, J. J., and E. R. Robertson. “Nasir al-Din al-Tusi.” MacTutor History of Mathematics Archive. https://mathshistory.st-andrews.ac.uk/Biographies/Al-Tusi_Nasir/.

“Medici Oriental Press.” Wikipedia. https://en.wikipedia.org/wiki/Medici_Oriental_Press.

Nasr, Seyyed Hossein. “Al-Ṭūsī, Muḥammad Ibn Muḥammad Ibn Al-Ḥasan Usually Known as Naṣir Al-Dīn.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, xiii:508–513. New York: Scribner, 1972.

Index to Mathematical Treasures

This 1482 version (Linda Hall Library call number QA31.E8587 1482) was the first edition of Euclid’s Elements to be printed, and was actually one of the first printed mathematical texts. It is in Latin, published by Erhard Ratdolt on May 25, 1482, in Venice, based on Campanus’ translation of Euclid’s Elements from Arabic, and contains 15 books rather than 13. Based on the number of surviving copies in libraries, Ratdolt printed more than the typical average 15th-century run of 300 copies. The copy at the Linda Hall Library of Science, Engineering & Technology was once owned by George Sarton, who is considered the founder of the history of science as an academic discipline. It contains marginal notes in Latin and bookworm holes.

The Pythagorean Theorem is Proposition 46 instead of 47.

For more images of Euclid’s Elements, printed by Ratdolt in 1482, visit the page “Mathematical Treasures - Ratdolt's Euclid's Elements” by Frank J. Swetz in Convergence.

Images in this article were taken by the author at the Linda Hall Library of Science, Engineering & Technology and are used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

O'Connor, J. J., and E. F. Robertson. “Campanus of Novara.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Campanus/.

Norman, Jeremy. “Euclid's Elements, the Most Famous Textbook Ever Published (May 25, 1482).” http://www.historyofinformation.com/expanded.php?id=382.

Swetz, Frank J. “Mathematical Treasure: Ratdolt's Euclid's Elements.” Convergence (August 2012), DOI:10.4169/loci003904. http://www.maa.org/press/periodicals/convergence/mathematical-treasure-ratdolts-euclids-elements.

“George Sarton.” Wikipedia. https://en.wikipedia.org/wiki/George_Sarton.

Index to Mathematical Treasures

The 17th-century Italian mathematician and supporter of Galileo, Evangelista Torricelli, published only one book during his lifetime, Opera Geometria. The picture below is the title page of Lezione Accademiche d’Evangelista Torricelli or Academic Lectures of Evangelista Torricelli. This work (Linda Hall Library call number Q155.T69 1715) was published posthumously in 1715. It contains 12 lectures in Italian that Torricelli gave at various places, which were collected and published by Tommaso Bonaventuri. According to the Dictionary of Scientific Biography, most of the lectures were on physics, but one is “in praise of mathematics.”

Below is a picture of the title page.

]

The frontispiece contains a portrait of Torricelli.

A digital scan is available in the Linda Hall Library Digital Collections. For more on Torricelli’s Academic Lectures, visit the Convergence pages “Mathematical Treasure: Academic Lectures by Torricelli” and “Mathematical Treasure: Torricelli’s Academic Lectures,” both by Frank J. Swetz.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Gliozzi, Mario. “Torricelli, Evangelista.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, xiii:433–440. New York: Scribner, 1972.

O'Connor, J. J., and E. F. Robertson. “Evangelista Torricelli.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Torricelli/.

Index to Mathematical Treasures

The 17th-century Italian mathematician and supporter of Galileo, Evangelista Torricelli, published only one book during his lifetime. The image below is the title page of this 1644 work, Opera Geometria (Linda Hall Library call number QA33.T69 1644).

According to the Dictionary of Scientific Biography, “The volume, Opera Geometria, was divided into three sections: the first dealt with De sphaera et sphaeralibus libri duo; the second contained De motu gravium naturaliter descendentium et proiectorum (the writing submitted to Galileo for his opinion); and the third section consisted of De dimensione parabola. The work, soon known throughout Italy and Europe, had intrinsic value and, through its clear exposition, diffused the geometry of Cavalieri, whose writings were difficult to read.”

This next image is the start of the first section.

The page below is the start of a section on the squaring of the parabola.

The well-known solid of revolution with infinite surface area yet finite volume, known as Gabriel’s Horn or Torricelli’s Trumpet, made its first appearance in Opera Geometria.

For a portrait of Torricelli, visit the “Evangelista Torricelli’s Academic Lectures” page of Mathematical Treasures.

A digital scan is available in the Linda Hall Library Digital Collections. For more images of Torricelli’s Opera Geometrica, visit the page “Mathematical Treasure: Torricelli’s Geometry” by Frank J. Swetz in Convergence.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Gliozzi, Mario. “Torricelli, Evangelista.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, xiii:433–440. New York: Scribner, 1972.

O'Connor, J. J., and E. F. Robertson. “Evangelista Torricelli.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Torricelli/.

Index to Mathematical Treasures

Fibonacci, also known as Leonardo of Pisa or Leonardo Pisano, lived around 1170 to 1250. He was responsible for introducing to Europe the Hindu-Arabic numeration system that we use today when he published Liber Abaci in 1202. He also published at least five other works. The Linda Hall Library has a two-volume set, published in 1857, called Scritti de Leonardo Pisano, which translates as The Writings of Leonardo Pisano. This 19th-century edition by Baldassarre Boncompagni is the only complete collection of the surviving works of Fibonacci, and consists of the Latin text with no commentary. Volume 1 contains Liber Abaci, while Volume 2 is titled Practica Geometriae ed Opuscoli (Practical Geometry and Lesser Works). The “lesser” works are Flos, Epistola ad Magistrum Theodorum (a letter to the imperial philosopher Theodorus), and Liber Quadratorum (The Book of Squares).

According to the Dictionary of Scientific Biography, there are 12 surviving manuscript copies of Liber Abaci which date from the 13th through 15th centuries, with only three of the copies complete. In the Introduction to the English translation of Liber Abaci, L.E. Sigler writes, “There exist a number of manuscripts of Liber abaci in Europe which were examined by Boncompagni in preparing his definitive text. The Boncompagni text is complete and unambiguous.”

The following image is the title page of Liber Abaci in volume 1, although with the spelling – Liber Abbaci.

It is on page 2 that Fibonacci introduces the Hindu-Arabic numeration system.

Here is a close-up of the middle of the page, at the beginning of the first chapter.

The Latin translates as “These are the nine figures of the Indians 9, 8, 7, 6, 5, 4, 3, 2, 1. And so, with these nine figures, and with the symbol 0, which is called zephyr in Arabic, whatever number you please can be written, as is demonstrated below.”

Fibonacci goes on to explain how to write Roman numerals with this “new” system, providing some examples in a table near the bottom of page 3.

Next he explains some algorithms for performing arithmetic with Hindu-Arabic numerals, and on page 6, there are some addition and multiplication tables.

The infamous rabbit problem that led to what is now known as the Fibonacci sequence starts near the bottom of page 283 and continues on page 284. The Latin word for rabbit is “cuniculus.” Notice there is a typographical error in the section heading with the word “coniculorum” instead of “cuniculorum”.

As mentioned above, there is an English translation of Liber Abaci available; both a hardcover and a softcover edition from Springer, which makes it convenient for those who don’t know Latin to still study this work by Fibonacci. In fact, the author used the 19th-century Boncompagni version for his translation.

A complete digital scan of Liber Abaci (call number QA32.F55) is available in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

O'Connor, J. J., and E. F. Robertson. “Leonardo Pisano Fibonacci.” MacTutor History of Mathematics Archive. https://mathshistory.st-andrews.ac.uk/Biographies/Fibonacci/.

Sigler, L.E. Fibonacci’s Liber Abaci (A Translation into Modern English of Leonardo Pisano’s Book of Calculation). Springer, 2002.

Vogel, Kurt. “Fibonacci, Leonardo, or Leonardo of Pisa.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, iv:604–613. New York: Scribner, 1972.

“Fibonacci number.” Wikipedia. https://en.wikipedia.org/wiki/Fibonacci_number.

Index of Mathematical Treasures

Leonardo of Pisa, also known as Fibonacci, is best known for introducing to Europe the Hindu-Arabic numeration system that we use today when he published Liber Abaci in 1202. He also published at least five other works; one of which was called Practica Geometriae. The Linda Hall Library has a two-volume set, published in 1857, called Scritti de Leonardo Pisano, which translates as The Writings of Leonardo Pisano. This 19th-century transcription by Baldassarre Boncompagni is the only complete collection of the surviving works of Fibonacci, and consists of the Latin text with no commentary. While Volume 1 contains Liber Abaci, Volume 2 is titled Practica Geometriae ed Opuscoli (Practical Geometry and Lesser Works). The “lesser” works are Flos, Epistola ad Magistrum Theodorum (a letter to the imperial philosopher Theodorus), and Liber Quadratorum (The Book of Squares).

There is an English translation with commentary of Practica Geometriae, primarily based on the Boncompagni edition, available from Springer. According to the Dictionary of Scientific Biography, there are 9 surviving manuscript copies of Practica Geometriae. Boncompagni used one that was in the Vatican for the Scritti de Leonardo Pisano. Barnabas Hughes, in the prequel background material to his English translation, writes, “Fibonacci wrote De practica geometriae for these artisans [surveyors], a fitting complement to Liber Abaci. Beginning with the definitions and constructions found early in Euclid’s Elements, Fibonacci instructed his reader how to compute with Pisan units of measure, find square and cube roots, determine dimensions of both rectilinear and curved surfaces and solids, work with tables for indirect measurement, and perhaps fire the imagination of builders with analyses of pentagons and decagons. His work exceeded what readers would expect for the topic, particularly with lists of units of measurement and the many practical problems that exemplify their use.” (p. xvii)

The following image is the title page of Practica Geometriae ed Opuscoli in volume 2 of Scritti de Leonardo Pisano.

Chapter 1 contains 25 solved problems and 12 theorems. It starts with problems of finding the area of rectangular fields with the dimensions given. For example, the page below has the problem of finding the area of a rectangular field that is 17 rods and 3 feet on one side and 28 rods and 4 feet on the other. There is a figure to accompany the explanation which uses the distributive law, like the FOIL method for binomial multiplication.

Below is a picture from Chapter 7, which deals with finding heights using similar triangles—which would nicely supplement secondary school geometry curriculum.

As mentioned above, there is an English translation of Practica Geometriae available, which makes it convenient for those who don’t know Latin to still study this work by Fibonacci. In fact, the author used the 19th-century Boncompagni version for his translation.

A complete digital scan of Practica Geometriae ed Opuscoli (call number QA32.F55) is available in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Hughes, Barnabas. Fibonacci's De practica geometrie. Springer, 2008.

O'Connor, J. J., and E. F. Robertson. “Leonardo Pisano Fibonacci.” MacTutor History of Mathematics Archive. https://mathshistory.st-andrews.ac.uk/Biographies/Fibonacci/.

Vogel, Kurt. “Fibonacci, Leonardo, or Leonardo of Pisa.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, iv:604–613. New York: Scribner, 1972.

Index of Mathematical Treasures

The image below is the title page of A Panegyric upon Sir Isaac Newton, an English translation of a tribute to Newton by the Frenchman Bernard de Fontenelle (1657–1757). This 34-page work was published in 1728, the year after Newton died, and is based on an obituary notice Fontenelle presented to the Royal Academy of Sciences in Paris.

Beginning in 1697, Fontenelle served as the permanent secretary of the Academy of Sciences in Paris for 42 years.  He was also a poet and was known for his writing ability. This obituary in tribute to Newton is one of 69 such “éloges” that Fontenelle wrote. These 69 obituaries, including those of Newton and Leibniz, can be found in the Histoire du renouvellement de l'Académie des Sciences (Paris, 3 vols., 1708, 1717, 1722).  (A copy of this history of the Academy of Sciences is at the Linda Hall Library.) 

A Panegyric upon Sir Isaac Newton contains a detailed biography of Sir Isaac Newton, beginning with his birth and education, continuing with Newton’s contributions to mathematics and science, and concluding with a description of the man Newton, his death, and his estate. For example, an explanation is included on how Newton was able to find areas and centers of gravity of many curves using infinite series before Mercator published finding the area of a hyperbolic segment using an infinite series in 1668. The image below shows Fontenelle’s description of the infamous Newton-Leibniz Calculus Controversy.

Two other works are bound with this copy of A Panegyric upon Sir Isaac Newton:

1. Geometry no friend to infidelity : or, A defence of Sir Isaac Newton and the British mathematicians, in a letter to the author of The analyst ... by Philalethes Cantabrigiensis (a pseudonym for James Jurin).
2. The Analyst, by Bishop George Berkeley  (more on Berkeley’s The Analyst can be found on Convergence).

A complete digital scan of A Panegyric upon Sir Isaac Newton is available in the Linda Hall Library Digital Collections. The call number is QA35 .B47 1734.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

Francesco Algarotti was an Italian polymath, philosopher, and author during the Age of the Enlightenment. One of his books, Il newtonianismo per le dame ovvero dialoghi sopra la luce e i colori (Newtonianism for the ladies, or dialogues on light and colours), was instrumental in popularizing Newtonianism in continental Europe. The book consists of a series of six conversations in which Newton’s ideas and experiments on light and colors are explained to a fictional marchioness. The first edition was published in 1737, missing the usual permissions, and with a forged imprint of Naples on the title page. According to Massimo Mazzotti's "Newton for ladies:  gentility, gender, and radical culture," “due to the intervention of religious authorities Algarotti’s radical Newtonianism became gradually less visible in subsequent editions and translations.” The Linda Hall Library has three editions: the first 1737 Italian edition (which was on the Roman Catholic church’s 1739 list of prohibited books), a 1738 French edition (available online at https://catalog.lindahall.org/discovery/delivery/01LINDAHALL_INST:LHL/1284377900005961), and a 1739 Italian edition. Another interesting thing about the first edition is the frontispiece, which is a portrait of Algarotti and Émilie du Châtelet portraying the characters in the book. (Algarotti spent some time with Émilie du Châtelet and Voltaire at her estate of Cirey while he was finishing the book.)

The title page of the first edition:

A complete digital scan of the 1737 first edition in Italian, Il Newtonianismo per le dame ovvero dialoghi sopra la luce e i colori (call number QC19 .A48 1737) is available in the Linda Hall Library Digital Collections, along with the 1738 French edition (call number QC19 .A5 1738), and the 1739 Italian edition (call number QC19 .A48 1739).

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Mazzotti, Massimo. "Newton for Ladies: Gentility, Gender and Radical Culture." The British Journal for the History of Science 37, no. 2 (June 2004): 119–146. Stable URL: http://www.jstor.org/stable/4028327.

“Francesco Algarotti.” Wikipedia. https://en.wikipedia.org/wiki/Francesco_Algarotti.

“Newtonianism.” Wikipedia. https://en.wikipedia.org/wiki/Newtonianism.

Index to Mathematical Treasures

Although not a mathematician by profession, François Viète (1540–1603) made several important contributions to mathematics. One such contribution was the introduction of more symbolism within algebra; Viète was one of the first to use letters to represent known and unknown quantities. Opera Mathematica, which is a collection of mathematical works by Viète, was published after his death by Franz Schooten in 1646. Below is the title page and the table of contents.

Viète is given credit for coining the term “coefficient” (Schwartzman, p. 48). It appears in the image below in the second sentence of paragraph 9.

The next Opera Mathematica image shows page 5 from Isagoge in Artem Analyticam (Introduction to the Analytical Art. An English translation of Isagoge can be found in an appendix to Jacob Klein’s book Greek Mathematical Thought and the Origin of Algebra.) The page starts with Lesson 1 (To add a magnitude to a magnitude), followed by Lesson 2 (To subtract a magnitude from a magnitude), and then the beginning of Lesson 3 (To lead\multiply a magnitude to a magnitude). Notice that near the end of each of the first two lessons, it is written that analysts are in the habit of using the symbols + and – for addition and subtraction, respectively.

Below is a picture of the page where Viète introduced the use of letters to represent quantities. He used vowels for unknowns or “sought after” values and consonants for known values.

Also notice in the above picture, near the top, that a fraction bar is used as notation for division.

Although Viète distinguished between magnitude and number, we see in the image below, paragraph 25, that Viète discussed “formulas of equations in which ‘cubes’ are equated to ‘solids,’ ‘squared-squares’ to ‘plane-planes’” (English translation from Klein, p. 352).

The above image is the last page of Viète’s Isagoge in Opera Mathematica. It concludes with an interesting quote about the goal of the analytical art: “NULLUM NON PROBLEMA SOLVERE,” or “TO LEAVE NO PROBLEM UNSOLVED” (English translation from Klein, p. 353).

The next two Opera Mathematica images are from Viète’s work Zeteticorum libri quinque, which consists of a collection of problems from Diophantus with solutions using Viète’s methods. These two pages contain the problem to find three right triangles with equal area. Notice the notation of an overbar used as a grouping symbol, instead of parentheses as used today, while multiplication is represented by “in.” Using modern notation and the Pythagorean Theorem, the first triangle on p. 71 (the second image below) gives \( (A^2 – B^2)^2 + (2AB)^2 = (A^2+B^2)^2 \). According to the Dictionary of Scientific Biography, “This innovation [of using A quadratus, A cubus, … to represent \( x^2, x^3, … \)], considered one of the most significant advances in the history of mathematics, prepared the way for the development of algebra,” and the shortening of quadratus to q occurred in the 1646 Opera but not in the original Zeteticorum (Busard, pp. 19 & 21).

A complete digital scan of Viète’s Opera Mathematica is available in the Linda Hall Library Digital Collections. The call number is QA33.V5. 

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Busard, H.L.L. “Viète, François.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, xiv:18–25. New York: Scribner, 1972.

Klein, Jacob. Greek Mathematical Thought and the Origin of Algebra. Dover Publications, 1968.

Schwartzman, Steven. The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. Mathematical Association of America, 1994.

Index to Mathematical Treasures

The following image is the title page of Discourses and Mathematical Demonstrations Concerning Two New Sciences; or Discorsi e Dimostrazioni Matematiche intorno à due nuoue Scienze by Galileo Galilei. This work was published in 1638 and was Galileo’s final published work.

The two “new sciences” discussed in the book are strength of materials and kinematics.  The book consists of four dialogues among Salviati, Sagredo and Simplicio.  The images below show some dialogue from early in the book.  The image on the left is from the original Italian version while the one on the right is from a 1730 English translation.

Here is the title page of the 1730 English translation.

If one visits the Linda Hall Library in person, it is possible to compare these two versions side-by-side.  The images below show how Galileo presented the science of the strength of materials as related to the law of the lever.

 

Here is another image from Dialogue II.

Below is a page about the center of gravity of a parabolic conoid.

Images and information about another copy of Galileo’s Two New Sciences are also available in Convergence.

A complete digital scan of the Italian 1638 edition of Galileo’s Two New Sciences is available in the Linda Hall Library Digital Collections. The call number is QA33 .G2 1638. A scan of the 1730 English translation is also available in the Linda Hall Library Digital Collections. The call number is QA33 .G22 1730.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Drake, Stillman. “Galilei, Galileo.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, v:237–249. New York: Scribner, 1972.

Index to Mathematical Treasures

The following image is the title page of The Analyst; or a Discourse Addressed to an Infidel Mathematician by Bishop George Berkeley. This work was published in 1734, the same year that Berkeley was appointed the Bishop of Cloyne in Ireland.

Bishop Berkeley is known for his attacks on Newton’s calculus, and The Analyst was the first of several publications containing his arguments that the calculus had weak foundations. These arguments helped instigate work on making the foundations more rigorous by others such as Colin Maclaurin and the Bernoullis.

The image below shows a page from the table of contents of The Analyst. Notice the title of Chapter 34–By what inconceivable Steps finite Lines are found proportional to Fluxions. Mathematical Infidels strain at a Gnat and swallow a Camel.

 

It is in Chapter 34 that Berkeley’s well-known quote about fluxions being “ghosts of departed quantities” can be found.

This page shows the dot notation being used for the derivative.

On page 32, meanwhile, we see the differential notation being used.

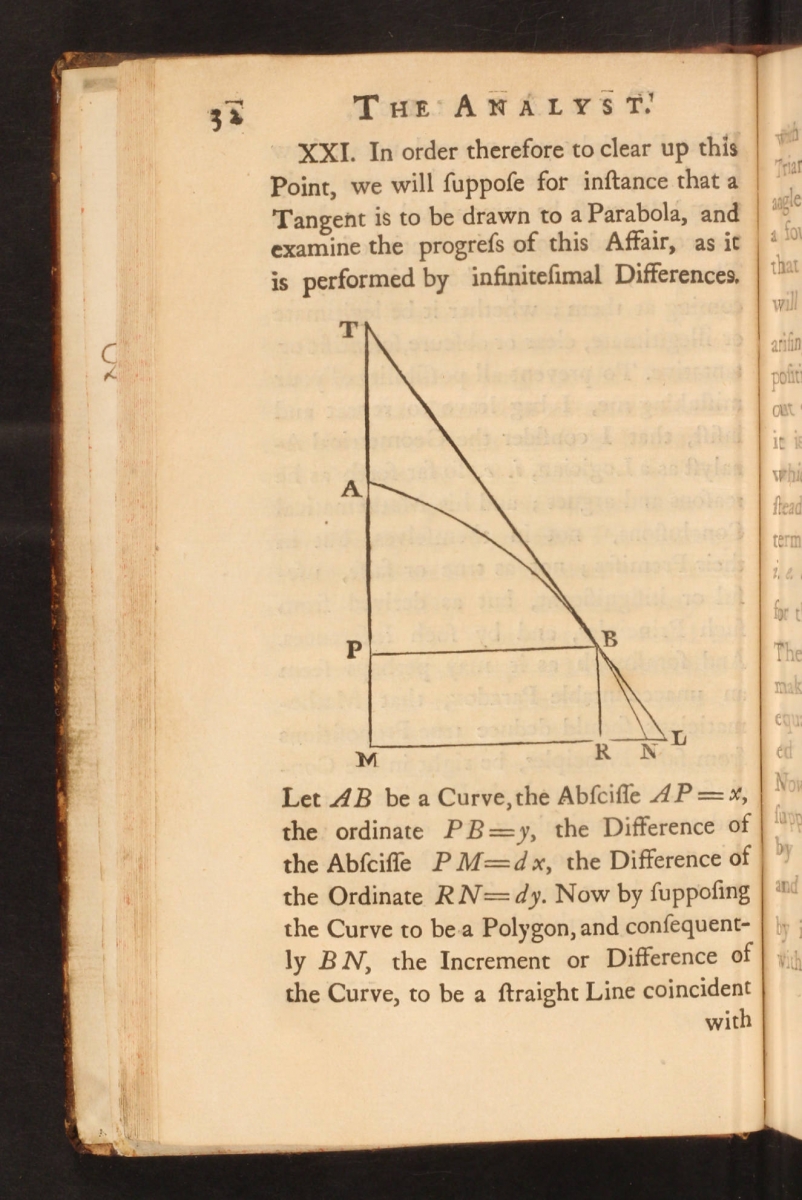
Below are two more pages from The Analyst.

The copy of the book at the Linda Hall Library may have been owned by Thomas Clarke, Esquire, of Knedlington, a small hamlet of East Riding, Yorkshire, England. He was a member of the Camden Society, which published new editions of rare or unpublished works.

Two other works are bound with this copy of The Analyst:

• Geometry no friend to infidelity : or, A defence of Sir Isaac Newton and the British mathematicians, in a letter to the author of The analyst ... by Philalethes Cantabrigiensis (a pseudonym for James Jurin), London, 1734.
• A panegyric upon Sir Isaac Newton / translated from the French, pronounced by Mr. Fontenelle before the Royal Academy of Sciences at Paris, by Andrew Reade, with remarks by James Wilson, London, 1728.

Images of a later edition of Bishop George Berkeley’s The Analyst are also available in Convergence.

A complete digital scan of The Analyst is available in the Linda Hall Library Digital Collections. The call number is QA35 .B47 1734.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

Written by Thomas Harriot, Artis Analyticae Praxis (Practice of the Art of Analysis) was published in 1631, ten years after Harriot’s death. According to Katz and Parshall, “a convert to Viète’s ideas, the Englishman [Harriot] extended them by making algebraic arguments even more symbolic. ... Harriot’s notational innovations made Viète’s ideas an even more useful tool for manipulating and solving equations. [Then] Fermat … fashioned these ideas into a tool for dealing algebraically with curves in the plane.” (Katz & Parshall, pp. 249, 252) Below is the title page of Artis Analyticae Praxis.

Next are images of three pages with examples of arithmetic operations using variables.

   

   

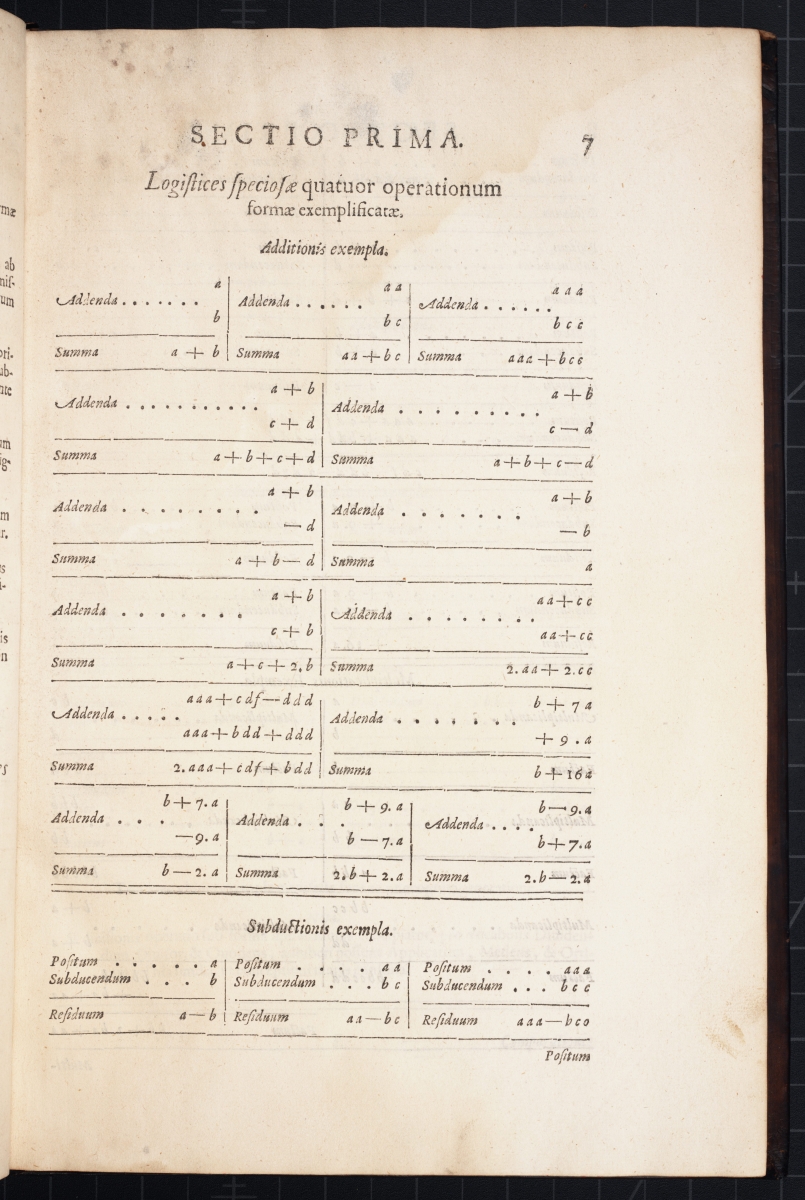
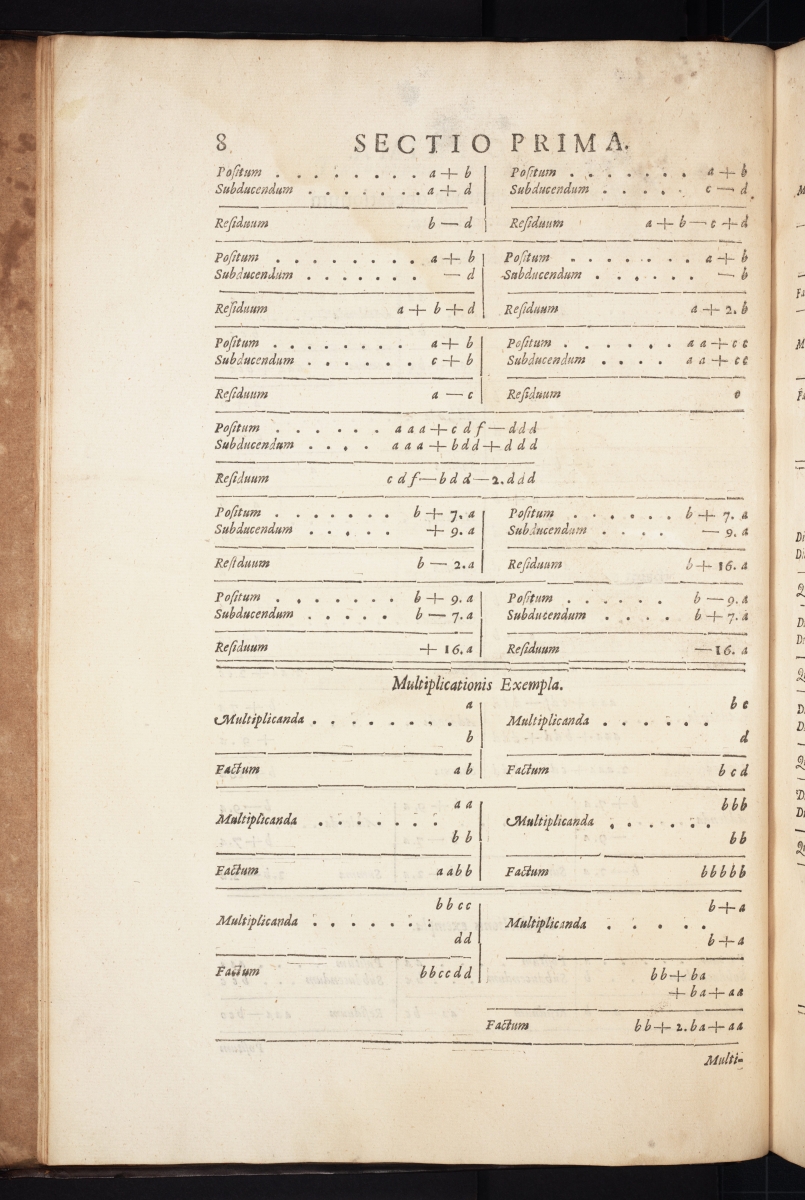
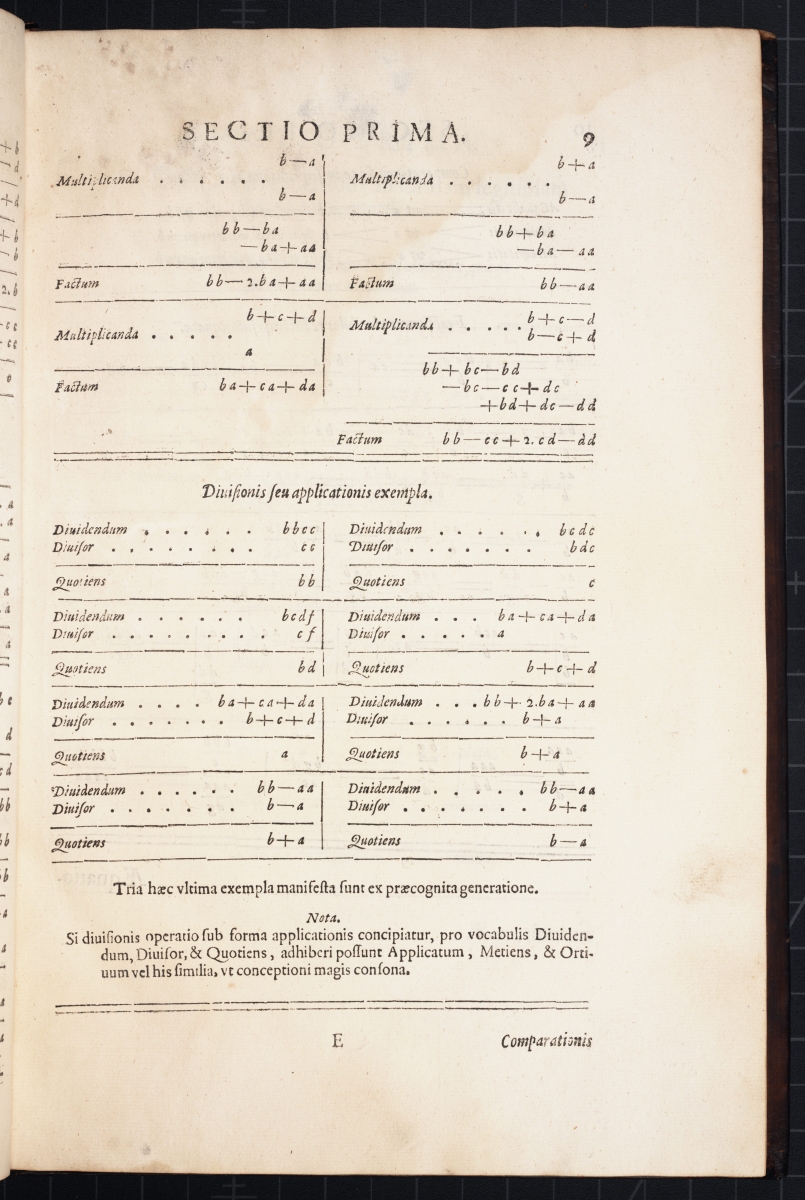
The image below shows the derivation of the quadratic equation \( a^2 – ba + ca = bc \) from expanding \( (a – b)(a + c) = 0 \).

The image below shows reducing the trinomial \( a^3 – 3ba^2 + 3b^2a = b^3 + c^3 \) to the binomial \( a^3 – 3bca = b^3 + c^3 \).

Images from another copy of the 1631 edition of Artis Analyticae Praxis can also be found in Convergence.

English translations of Harriot’s Artis Analyticae Praxis are available on the web and in print.

A complete digital scan of Artis Analyticae Praxis is available in the Linda Hall Library Digital Collections. The call number is QA33.H37 1631.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Katz, Victor J., and Karen Hunger Parshall. Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century. Princeton: Princeton University Press, 2014.

Index to Mathematical Treasures

 

The above image is the title page of a 1535 edition of Geometrei by Jacob Kőbel. Images from a 1608 edition can also be found on Convergence, as well as an explanation of the second graphic on this title page. The woodcut illustrates determining a unit of measure called a “rood” by lining up the feet of 16 men.

Today Kőbel’s Geometrei, with its focus on measurement, is classified as a surveying book rather than a geometry book. The picture below shows measuring the height of a tower with Jacob's staffs.

In the next picture, a mirror (spiegel in German) is shown in a diagram with similar triangles.

The page below contains information about measuring fields and one of the graphics used on the title page.

A complete digital scan of Kőbel’s Geometrei, call number TA544 .K63 1535, can be found in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

German mathematician and astronomer Johann Stoeffler (or Johannes Stöffler) wrote an influential book with the title Elucidatio fabricae vsusque astrolabii, on how to make and use an astrolabe. First published in 1513, the book went through 16 editions by the year 1620. According to the Oxford Museum of the History of Science, it was “one of the most influential books on a scientific instrument ever to be published. . . . Many authors of the many books on mathematical instruments to be published in the 16th century followed Stöffler’s example.”

The image below is the title page of a 1524 edition at the Linda Hall Library of Science, Engineering, and Technology in Kansas City, Missouri. The call number is CE73.S7 1518.

The first part of the book deals with the construction of astrolabes. The next image is the start of a section in the Second Part of the book about various types of geometry, both theoretical and practical. Near the center of the page is a listing of different units of measure including digit (finger), palmus (hand), pes (foot), cubit, passus (pace), pertica (perch or rod), stadium (furlong), miliarium (mile), and leuca (league). In the center of the page are line segments showing the length of a digit and hand, and on the side of the page is a line segment for a foot. The relations among the units are given: a hand is 4 digits, a foot is 4 hands (today a foot is considered 3 hands), a cubit is a foot and a half, a pace is 5 feet (today a pace is 2.5 feet), a rod is 10 feet (today a rod is 16.5 feet), a stadium/furlong is 125 paces (named after stando, the length Hercules could run in one breath or the length after which youth running would stop for a rest), a mile is 8 furlongs or 1000 paces (hence its name), and a league is a mile and a half or 1500 paces.

The second part of the book then gives instructions on taking measurements of objects such as towers and wells using an astrolabe, and includes many figures such as the one below which shows a man using an astrolabe to measure the height of a tower based on the length of its shadow.

A digital scan is available in the Linda Hall Library Digital Collections. An English translation of the 1553 edition of Stoeffler’s Elucidatio exists. A copy of the translation is also available at the Linda Hall Library, so one could compare the Latin 1524 edition side-by-side with an English translation of the 1553 edition.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Stoeffler's Elucidatio. Paris, 1553. Translated and edited by Alessandro Gunella and John Lamprey. Cheyenne, Wyo.: Classical Science Press, 2007.

Index to Mathematical Treasures

Englishman John Caswell wrote a book with the title A Brief (but full) Account of the Doctrine of Trigonometry, Both Plain and Spherical, which was published in 1685. Caswell was a student of John Wallis and held the Savilian Chair of Astronomy at Oxford from 1709 to 1712.

The page below shows the first page, which contains a list of symbols that Caswell used in this trigonometry textbook. Some, but not all, of the symbols are still in use today.

A complete digital scan of Caswell’s Trigonometry  is available in the Linda Hall Library Digital Collections. The call number is QA33 .W343 1685. 

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index of Mathematical Treasures

The image below is the title page of Geometry no friend to infidelity: or, A defence of Sir Isaac Newton and the British mathematicians, in a letter to the author of the Analyst. The title page lists the author as Philalethes Cantabrigiensis, but it is believed that the author is actually James Jurin.

Jurin (1684–1750) was a physician and scientist who did work with the smallpox vaccination and capillaries. He was a strong supporter of Sir Isaac Newton; this 84-page work was published in 1734 in reaction to the Bishop George Berkeley’s The Analyst, which had appeared earlier that year. (It was in The Analyst that Berkeley questioned whether fluxions were the “ghosts of departed quantities.” More on Berkeley’s The Analyst can be found on Convergence.) According to Carl Boyer's The History of the Calculus and Its Conceptual Development, this work by Jurin contained weak arguments. However, it was the first of about 30 such works over the next 7 years written in response to the early logical issues in calculus raised by Berkeley. These arguments actually led to work by others, including Colin Maclaurin and the Bernoullis, on making the foundations of calculus more rigorous.

The image below shows the first page after the Table of Contents and the start of the response to Bishop Berkeley.

Two other works are bound with this copy of A defence of Sir Isaac Newton:

1. The Analyst, by Bishop George Berkeley.
2. A panegyric upon Sir Isaac Newton / translated from the French, pronounced by Mr. Fontenelle before the Royal Academy of Sciences at Paris, by Andrew Reade, with remarks by James Wilson. (More on this eulogy of Newton can be found on Convergence.)

A complete digital scan of Geometry no friend to infidelity, along with A Panegyric upon Sir Isaac Newton, is available in the Linda Hall Library Digital Collections. (The scan of Geometry no friend to infidelity comes first with A Panegyric upon Sir Isaac Newton starting after page 84.) The call number is QA35.B47 1734.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

• Boyer, Carl B. The History of The Calculus and Its Conceptual Development. Dover, 1959.
• Huffman, Cynthia J. “George Berkeley's The Analyst.” Convergence (July 2017).
• Swetz, Frank J. “Mathematical Treasure: Berkeley's Critique of Calculus.” Convergence (August 2015).
• “James Jurin.” Wikipedia. https://en.wikipedia.org/wiki/James_Jurin.

Index to Mathematical Treasures

Joseph-Louis Lagrange (1736–1813) was born Giuseppe Lodovico Lagrangia in Turin, in what is now northern Italy. Lagrange contributed to several branches of mathematics, including the beginnings of abstract algebra. Below is an image of the title page from the 1808 edition of his Traité de la Résolution des Equations Numérique de tous les degrés.

Originally published in 1798, the 1808 “noevelle/new” edition contained revisions and more notes, making it the more widely used edition. The title can be translated as A Treatise on the solution of numerical equations of all degrees, indicating that the book deals with numerical solutions to equations. However, exact solutions to polynomial equations were also discussed, including a summary of Lagrange’s groundbreaking 1770 paper "Réflexions sur la résolution algébrique des équations" (published in the memoirs of the Berlin Academy of Sciences), which noted historian Israel Kleiner called one of the “four major sources in the evolution of group theory.” The first page of this summary is below.

The mathematical notation is interesting in this work. Below is a picture of page 2, which shows Lagrange representing general polynomial equations as a product of linear factors.

In the next picture, from Note 5 on Newton’s Method for approximating roots of polynomial equations, a general polynomial is shown in expanded form.

 

The pictures below are from Note 7 on the method of Alexis Fontaine for finding solutions of cubics, which shows notation for nonreal complex roots; Note 10 where the Greek capital sigma was used for summations; and from Note 12, depicting sequences of fractions starting with 1/0.

A complete digital scan of the 1808 edition of Lagrange’s Traité de la Résolution des Equations Numérique is available in the Linda Hall Library Digital Collections. The call number is QA218.L33 1808.

Janet Heine Barnett has created a project for students based on this primary source as part of the TRIUMPHS project.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Kleiner, Israel. “The Evolution of Group Theory: A Brief Survey.” Mathematics Magazine 59, no. 4 (1986): 195-215. doi:10.2307/2690312.

Wussing, Hans. The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory. Dover Publications, 2007.

Index to Mathematical Treasures

Luca Pacioli was an Italian mathematician and friend of Leonardo da Vinci. He is especially known for Sūma de Arithmetica Geometria Proportioni & Proportionalita, a 600-page collection of the mathematics known at the time, published in 1494. The second work for which Pacioli is known is Divina Proportione (Linda Hall Library call number QA464.P32 1509). Although not stated explicitly, it is generally believed that Leonardo da Vinci did the illustrations for this 1509 book. Pacioli taught da Vinci mathematics and the two became close friends. In fact, Pacioli is the first to describe da Vinci’s famous The Last Supper painting in print, praising it in the dedication page of Divina Proportione. (Pedretti, p. 180) Below is the title page of Divina Proportione.

The book contains geometric studies of capital letters, including M, which was the iconic logo of the Metropolitan Museum of Art in New York from 1971 to 2016.

There are 59 illustrations of polyhedra; some of which are solid, and some, like the one below, which are skeletal, making it easier to see edges and vertices.

The 1509 publication actually contains 3 works that were completed in 1498. The first is Divina Proportione; the second contains geometry related to architecture, including the golden ratio; and the third is an Italian translation of a work by Italian artist Piero della Francesca. There are two surviving manuscript versions, and it is possible to purchase facsimile editions.

For more information and images of Pacioli’s Divina Proportione, visit the following pages:

• "Mathematical Treasures - De Divina Proportione, by Luca Pacioli" by Frank J. Swetz in Convergence, with two images from the copy at Columbia University’s Butler Library.
• "Mathematical Treasure: De Divina Proportione" by Frank J. Swetz in Convergence, with three images from the copy at the University of Oklahoma Library.
• “Leonardo da Vinci's Geometric Sketches” by Frank J. Swetz in Convergence, which displays illustrations of the Platonic solids by Leonardo Da Vinci from a facsimile of Pacioli's manuscript version of De Divina Proportione.

Images in this article were taken by the author at the Linda Hall Library of Science, Engineering & Technology and are used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Medieval Manuscript Facsimiles for Book Collectors & Libraries. https://www.facsimilefinder.com/.

O'Connor, J. J., and E. F. Robertson. “Luca Pacioli.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Pacioli/.

O'Connor, J. J., and E. F. Robertson. “Piero della Francesca.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Francesca/.

Pedretti, Carlo. Leonardo da Vinci: The Complete Works. David & Charles Books, 2013.

Index to Mathematical Treasures

The Italian mathematician Luca Pacioli, who is known for publishing an influential compendium of 15th-century mathematics, titled Sūma de Arithmetica Geometria Proportioni & Proportionalita, and a book illustrated by Leonardo da Vinci, titled Divina Proportione, also published a Latin translation of Euclid’s Elements (Linda Hall Library call number QA31.E857 1509) in 1509. Below is the title page.

Notice that the title mentions Euclid of Megara. During the European Middle Ages Euclid of Alexandria (ca 325 BC–ca 265 BC) was often confused with the Greek philosopher Euclid of Megara (ca 435 BC–ca 365 BC).

The name of Campanus is also mentioned on the title page (end of 4th line to start of 5th line). This edition of Euclid’s Elements is based on Johannes Campanus’ earlier (around 1260) Latin translation, with annotations added by Pacioli. There are sections in the work labeled “Verba Campani” or “The Words of Campanus,” as in the image below.

Like the translation by Campanus, which was the standard for over 200 years, Pacioli’s version of Euclid contains 15 books. The picture below shows the end of Book 14 (decimusquartus) and the start of Book 15 (decimusquintus).

The next image is of the definitions on the first page of Book 1.

This page shows two figures (the top two) to accompany the Pythagorean Theorem, Proposition 46.

The copy of the book at the Linda Hall Library was at one time in the library of a member of the well-known Florentine family Strozzi. Below is the page with the ownership written at the top and the family coat of arms at the bottom of the page, followed by a close-up of the coat of arms.

For more images of Pacioli’s Elements, visit the page “Mathematical Treasure: Pacioli's Elements of Euclid” by Frank J. Swetz in Convergence.

A complete digital scan is available in the Linda Hall Library Digital Collections.

Images in this article were taken by the author at the Linda Hall Library of Science, Engineering & Technology and are used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

O'Connor, J. J., and E. F. Robertson. “Campanus of Novara.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Campanus/.

O'Connor, J. J., and E. F. Robertson. “Euclid of Alexandria.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Euclid/.

O'Connor, J. J., and E. F. Robertson. “Luca Pacioli.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Pacioli/.

“Euclid of Megara.” Wikipedia. https://en.wikipedia.org/wiki/Euclid_of_Megara.

“Strozzi family.” Wikipedia. https://en.wikipedia.org/wiki/Strozzi_family.

Index to Mathematical Treasures

The Italian mathematician Luca Pacioli published an influential compendium of the mathematics known at the time, titled Sūma de Arithmetica Geometria Proportioni & Proportionalita (Linda Hall Library call number QA32.P32 1494), in 1494. The book contains over 600 pages of densely packed type along with figures. The image below is the title page of the 1494 edition, published in Venice. There was also an edition published in 1523 in Toscolano. The 1494 volume at the Linda Hall Library has a vellum cover and handmade paper.

According to David Eugene Smith in Rara Arithmetica, “This volume, the first great general work on mathematics printed, includes treatises on arithmetic, algebra, and geometry, each being considered from a somewhat scientific rather than practical standpoint.” (p. 56)

The verso of folio 29 shows the start of two and a half pages of multiplication tables.

Later, on the verso of folio 72, there is a multiplication table resembling those that appear in modern elementary curricula.

Summa was the first printed book to contain a chart of how to represent numerals with fingers (verso of folio 36).

Pacioli is sometimes called the “Father of Accounting” since Summa may contain the first published explanation of double-entry bookkeeping. As with most of the material in Summa, Pacioli is not presenting original work. Double-entry bookkeeping had been in use in Venice for around two hundred years prior to the publication of Summa. Below is the first page of the section, namely the eleventh tractatus of the ninth distinction titled Particularis de pomputis et scripturis, about double-entry bookkeeping.

As influential as Pacioli’s Summa has been, the section on double-entry bookkeeping is the only part of the work with a readily available English translation.

A complete digital scan of Summa is available in the Linda Hall Library Digital Collections.

For more images of Pacioli’s Summa, visit the Convergence article, “Mathematical Treasures - Pacioli’s Summa," by Frank J. Swetz and Victor J. Katz.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

O'Connor, J. J., and E. F. Robertson. “Luca Pacioli.” MacTutor History of Mathematics archive. https://mathshistory.st-andrews.ac.uk/Biographies/Pacioli/.

Schemmann, Michael, editor. The Rules of Double-Entry Bookkeeping (English translation of Particularis de computis et scripturis by Luca Pacioli). IICPA Publications, 2010.

Smith, David Eugene. Rara Arithmetica: A Catalogue of the Arithmetics Written Before the Year 1601. 1908. Reprint, Cosimo Classics, 2007.

Index to Mathematical Treasures

Billed as the first differential calculus textbook, Analyse des Infiniment Petits, Pour l’intelligence des lignes courbes (Analysis of the infinitely small to understand curved lines), was written by Guillaume François Marquis de l’Hospital. The first edition of this French book was published in 1696, with other editions appearing posthumously from 1716 to 1781. The book is credited with introducing many French mathematicians and others to the differential calculus of Leibniz. In the preface, l'Hôpital mentions that he focuses on just differential calculus since Leibniz was writing a book (which was never finished) on integral calculus. L'Hôpital also credits Johann Bernoulli, whom he had hired to teach him the calculus of Leibniz. In fact, there is some question as to how much of the material in the Analyse is due to l'Hôpital and how much to Johann Bernoulli. Below is a portrait of the author from the frontispiece of the first edition. Notice his last name is spelled as l’Hospital, although today it is more often seen in a modernized form, l'Hôpital.

Next is a copy of the title page.

The images below show the two pages of the Table of Contents of the Analyse.  Notice the title of Chapter 1 which translates as In which we give the Rules of the calculus of Differentials.

Below, the first page of the text begins with definitions of variable and constant.

Here on page 5 is Proposition III, the quotient rule.

While on page 15, we see an example of drawing a tangent line to y³ – x³ = axy with the accompanying figure.

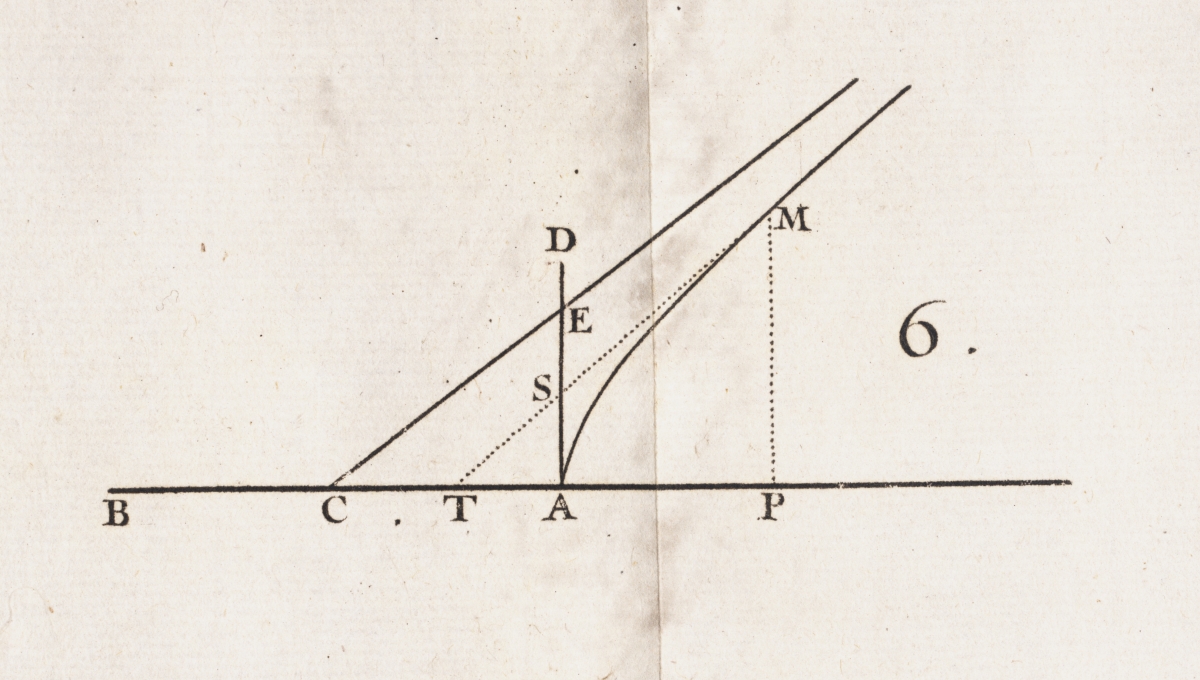
Below are two more pages from the Analyse. Page 55 is the start on the section about inflection points and page 89 looks at the logarithmic spiral.

The discussion of what is now known as l’Hôpital’s rule is found on pages 145–147.

Images from another copy of the 1696 edition of l’Hôpital’s Analyse can also be found in Convergence.

An English translation with commentary was published in 2015.

A complete digital scan of the Analyse is available in the Linda Hall Library Digital Collections. The call number is QA302 .L49 1696.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Boyer, Carl. The History of the Calculus and Its Conceptual Development. Dover, 1949, pp. 238, 241.

Bradley, Robert E., Salvatore J. Petrilli, and C. Edward Sandifer. L’Hôpital's Analyse des infiniments petits, An Annotated Translation with Source Material by Johann Bernoulli. Birkhäuser, 2015.

Underwood, Edward Dudley (Ed.). Readings for Calculus, Volume 5 of Resources for Calculus, MAA Notes Volume 31. The Mathematical Association of America, 1993, pp. 60–63.

Index to Mathematical Treasures

The following image is the title page of volume 1 of Maria Gaetana Agnesi’s Instituzioni Analitiche ad uso della gioventù italiana (Foundations of Analysis for the Use of Italian Youth), published in 1748 in Italian in Milan, and a two-volume work on algebra and calculus. The book was written as a teaching text and received high praise from a committee of the Académie des Sciences in Paris for uniformly synthesizing and clarifying the work of others on calculus. According to the Dictionary of Scientific Biography, “this book won immediate acclaim in academic circles all over Europe and brought recognition as a mathematician to Agnesi.”

The work was translated into English by Rev. John Colson (who learned Italian just so he could translate Analytical Institutions) and published in 1801. Here is the title page of the English translation of Volume 1 and the start of a preface by the editor.

Today many people know of Agnesi due to a mistranslation of the name of a cubic curve she discusses in Analytical Institutions.

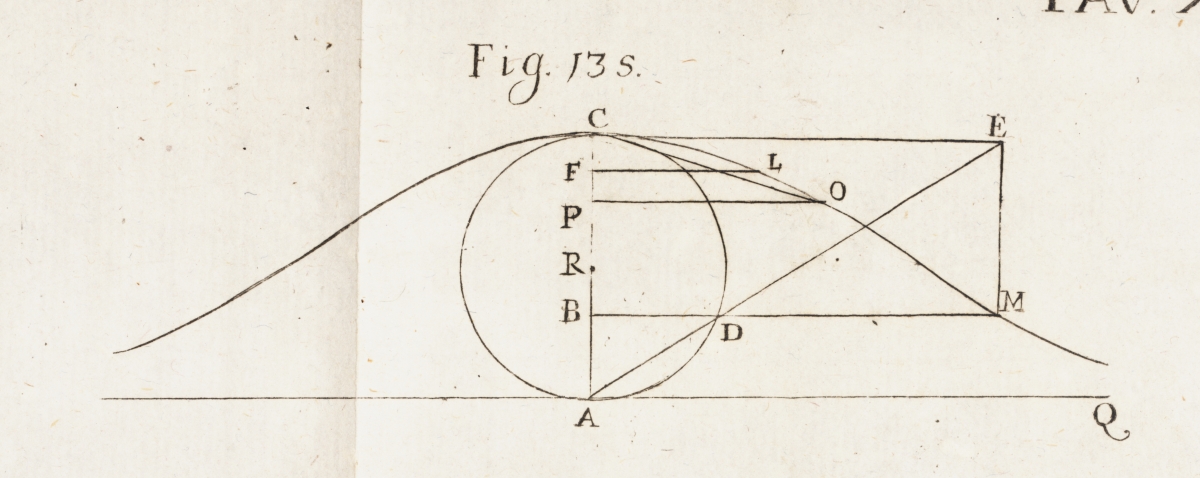
While Agnesi called this curve la Versiera, Colson translated it as the Witch and the curve became known commonly as the Witch of Agnesi. The first two images below are from the original Italian edition, followed by two images from the English translation.

Since the Linda Hall Library collections include both the original Italian version and the English translation, readers are able to take a look at the volumes side by side. In doing so, it is interesting to note that in the original Italian version, Agnesi uses the notation and terminology of Leibniz, while in the English translation, Colson uses Newton’s notation and terminology. For an example, see the images below from Section 28 of Volume 2.

   

The picture below from page 16 of volume 1 in Italian shows examples of polynomial multiplication.

Negative exponents are explained on page 56 and rational exponents on page 57.

For more images of Maria Agnesi’s Analytical Institutions, in both Italian and English, visit the page Mathematical Treasures - Maria Agnesi's Analytical Institutions, by Frank J. Swetz and Victor J. Katz, in Convergence.

Complete digital scans of of both Agnesi’s original Italian work, Volume 1 and Volume 2, and the English translation of Analytical Institutions, Volume 1 and Volume 2, are available in the Linda Hall Library Digital Collections. The call number for the original Italian version of Agnesi’s Analytical Institutions is QA35.A315 1748, while the English translation is QA35.A3 1801.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Kramer, Edna. “Agnesi, Maria Gaetana.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, i:75–77. New York: Scribner, 1972.

O'Connor, J. J., and E. F. Robertson. “Maria Gaëtana Agnesi.” MacTutor History of Mathematics archive. http://www-history.mcs.st-and.ac.uk/Biographies/Agnesi.html.

Swetz, Frank J., and Victor J. Katz. “Mathematical Treasures – Maria Agnesi's Analytical Institutions.” Convergence (January 2011). http://www.maa.org/press/periodicals/convergence/mathematical-treasures-maria-agnesis-analytical-institutions.

“Witch of Agnesi.” Wikipedia. https://en.wikipedia.org/wiki/Witch_of_Agnesi.

Index to Mathematical Treasures

Rafael Bombelli (1526–1572) was born in Bologna, in what is now Italy. Growing up in this area during the time of the controversy over the solution of cubic equations influenced Bombelli, who decided that a self-contained algebra book, which could be understood by a wide audience, was needed. The result was L'algebra parte maggiore dell’aritmetica divisa in tre libri, first published in 1572. The image below shows the title page of a 1579 edition titled L'algebra: opera di Rafael Bombelli da Bologna. Both editions were in Italian.

The names Cardano, Tartaglia, and Ferrari, important players in the cubic dispute, are mentioned on the fifth page of a section titled “Agli Lettori” or “To the Readers.” For instance, Bombelli praises Cardano's work but calls his writing obscure (oscuro). [See Stedall 2010, page 18 footnote, for a translation of the sentence.]

Above, on page 6, Bombelli explains some of his notation. In the image of page 70 below, Bombelli presents rules for multiplying with signed numbers, along with some examples.

In addition to being a comprehensive presentation of the algebra known at the time, L’algebra contained the first treatment of the arithmetic of complex numbers.

We see at the bottom of page 169 above, Bombelli presented rules for multiplying certain complex numbers.  These translate as:

A positive times a positive square root of a negative gives a positive square root of a negative.

A negative times a positive square root of a negative gives a negative square root of a negative.

A positive times a negative square root of a negative gives a negative square root of a negative.

A negative times a negative square root of a negative gives a positive square root of a negative.

A positive square root of a negative times a positive square root of a negative gives a negative.

A positive square root of a negative times a negative square root of a negative gives a positive.

A negative square root of a negative times a positive square root of a negative gives a positive.

A negative square root of a negative times a negative square root of a negative gives a negative.

Below is an image of page 188.  At the bottom of the page, Bombelli demonstrates cubing the complex number \( 3 + 4i \), by first squaring it, using distributivity, to get \( -7 + 24i \), which is then multiplied by another factor of \( 3 + 4i \) to yield \( (3 + 4i)^3  = -117 + 44i \).

A complete digital scan of the 1579 edition of Bombelli’s L’algebra is available in the Linda Hall Library Digital Collections. The call number is QA33 .B65 1579. Another copy of the 1579 printing is also available from Convergence.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Stedall, Jacqueline. From Cardano’s great art to Lagrange’s reflections: filling a gap in the history of algebra. European Mathematical Society, 2010, pp. 17–19, 211.

Index to Mathematical Treasures

Written by Gregor Reisch, Margarita philosophica cu[m] additionibus nouis (Pearl of Wisdom or Philosophical Pearl) was a popular 16th-century encyclopedia/textbook. It was first published in 1503; at least 15 editions appeared. The title page below is from an edition published in 1517, which, according to the subtitle, is the fourth revision. Images from another edition can also be found in Convergence.

The book is written in the form of a dialogue between a student and teacher, and it contains many woodcuts to illustrate the content. There are twelve chapters in the book, with each of the first seven devoted to one of the disciplines from the trivium (grammar, logic, and rhetoric) and quadrivium (arithmetic, geometry, music, and astronomy). Below is the frontispiece which shows these 7 liberal arts, followed by the woodcuts for the openings of each of these seven chapters.

The image below shows a counting board followed by an explanation and examples of how to represent numbers on the board. The word “denarius” is used for the markers. (A denarius was a silver coin equivalent to the value of “10 asses”.) Graphics in the right-hand margin illustrate the examples. The first illustrates 15, with a marker on the 10 line and another in the space between 1 and 10, representing 5. The second graphic demonstrates that if there are two markers in a space (“in spacio aliquo duos denarius”), they can be replaced by one marker on the next line up (“linea immediate superioze”). The third graphic shows 30 (“triginta”) with 3 markers on the 10 line, while the final graphic shows 259 as 200 + 50 + 5 + 4.

The next three pages are from the chapter on Geometry, and looking at the third one, we see that Reisch was using \( \frac{22}{7} \) for \( \pi \).

The woodcut below shows Ptolemy, wearing a crown, with Astronomy.

All of the above images came from a book that can be viewed in person at the Rare Book Room of the Linda Hall Library in Kansas City. The call number is AE25 .R44 1517. A complete digital scan of a 1508 edition of Margarita Philosophica is on GoogleBooks.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Ashworth, William B. Scientist of the Day – Gregor Reisch. Linda Hall Library, May 9, 2017. https://www.lindahall.org/gregor-reisch/.

Smith, David Eugene. Rara Arithmetica. 1908. Reprint; Cosimo Classics, 2007, pp. 82–84.

Index to Mathematical Treasures

Robert Simson (1687–1768) was a Scottish mathematician and chair of mathematics at the University of Glasgow. His work focused on restoring the existing partial versions of the ancient Greek geometers, such as Euclid and Apollonius. His restoration of Euclid’s Elements was especially influential. Images of a 1756 English first edition and an 1834 American edition of Simson’s The Elements of Euclid are available on Convergence.

The above portrait of Simson is from the frontispiece of his Opera and is one of the earliest images of the special academic gown worn by professors at the University of Glasgow.

Opera, published posthumously in 1776 by James Clow (Professor of Logic at Glasgow and Simson’s executor), contains four of Simson’s works which had not yet been published and an appendix. The title page can be seen below.

The next image is the section header page for the restoration by Simson of Apollonius’ De Sectione Determinata by using Pappus’ Lemmata. It was a work that Simson started early in his career and then completed in his later years.

De Sectione Determinata contains many problems like the one on page 71 pictured below, in which a number of points are given on a line, in this case 3, and another point is to be found that satisfies certain ratios.

According to William Trail, “the next, and certainly the most important portion of the posthumous volume, contains Dr. Simson’s discovery and illustration of the Porisms of Euclid.” [Trail 1812, p. 39] Porisms are “examples of Greek analysis which had been created to handle geometrical statements which fell between problems and theorems, such as classification of the properties of a geometrical locus.” [Ackerberg-Hastings 2000, p. 47] Below is the header page for this section of Opera.

The third work in Opera is De Logarithmis and may have been the last completed work of Simson. It is followed by De Limitibus Quantitatum et Rationum, the fourth part of Simson’s Opera. Although not complete, it was Simson’s attempt at a more rigorous treatment of fluxions than the one provided by Newton. The Opera concludes with an Appendix which contains samples of geometrical problems solved by Simson using methods of the ancient Greeks. Simson may not have intended these problems to have ever been published, but it was decided right before the Opera was printed to include a few examples.

A complete digital scan of the first edition of Simson’s Opera Quaedam Reliqua, call number QA3.S5 1776, can be found in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Ackerberg-Hastings, Amy. "Mathematics is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790–1840." PhD diss., Iowa State University, 2000. DOI:10.31274/rtd-180813-13933.

Dickson, Neil. "Tradition and Humour: The Academic Dress of the University of Glasgow." Transactions of the Burgon Society 12 (2012). DOI: 10.4148/2475-7799.1097.

Dickson, Neil. Department of Mathematics, University of Glasgow. Email correspondence, October 2019.

Trail, William. Account of the Life and Writings of Robert Simson, M.D.: Late Professor Mathematics in the University of Glasgow. London, 1812.

Index to Mathematical Treasures

The image below is the title page of The Elements of Euclid : viz. the first six books, together with the eleventh and twelfth, by the Scottish mathematician Robert Simson (1687–1768). A Latin version, also by Simson, was published on the same day in 1756. Although Simson attended the University of Glasgow with the intention of entering the ministry, he found his initial studies in theology unsatisfying, and after reading on his own, he developed a fascination with mathematics. In 1711, three days after graduating with his Master of Arts, he was appointed to the chair of mathematics at Glasgow, a position he would hold for 50 years. From the beginning, Simson’s mathematical interests focused on ancient Greek texts, especially in geometry, with the goal of perfecting the existing editions of works of ancient Greek geometers.

Thus, in the last page of the Preface, Simson stated, “Upon these Accounts it appeared necessary, and I hope will prove acceptable to all Lovers of Accurate Reasoning and of Mathematical Learning, to remove such blemishes, and restore the principal Books of the Elements to their original Accuracy.” Simson’s restoration of Euclid’s Elements would later appear in over 70 different editions or translations, a record held by very few mathematics books. In fact, even into the 20th century, modern geometry textbooks were greatly influenced by Simson’s version of Euclid. Images from an 1834 American edition of Simson’s The Elements of Euclid are also available on Convergence.

The next image shows the first page and begins with definitions. Notice that instead of “plane” Simson used the Latin term “superficies.”

Interestingly, Simson only has 3 postulates listed on page 6, instead of the usual 5.

The famous 5th postulate, also known as the Parallel Postulate, appears as Axiom 12.

In the Notes section at the back of the book, Simson does mention that his Axiom 12 is usually known as the 5th Postulate.

Below is an image of the Pythagorean Theorem from Book 1, Proposition 47.

A complete digital scan of The Elements of Euclid is available in the Linda Hall Library Digital Collections. The call number is QA31 .E88 1756.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Ackerberg-Hastings, Amy. "Mathematics is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790–1840." PhD diss., Iowa State University, 2000. DOI:10.31274/rtd-180813-13933.

Burnett, John. “Robert Simson’s Euclid and the Foulis Press.” Bibliotheck 11 (1983): 136–148.

Index to Mathematical Treasures

 

The image above is the title page of the 1735 first edition of Sectionum Conicarum by the Scottish mathematician Robert Simson (1687–1768). Images from an 1804 edition, which reprints an abbreviated English translation from the Latin, can also be found on Convergence.

From the beginning of his career, Simson’s mathematical interests focused on ancient Greek texts, especially in geometry, with the goal of perfecting the existing editions of works of ancient Greek geometers. This particular book complements Simson's restoration of Apollonius’ Conics, which was completed around the same time but not published until 1749. In both books, Simson used purely geometric methods and avoided using algebra.

Page 1 starts out with a section about the parabola.

In the next images, from pages 2 and 3, we see Proposition 2, which states that if a point is equidistant from the focus and directrix then it is on the parabola. The accompanying Figure 1 is from a fold-out page.

A complete digital scan of the first edition of Simson’s Sectionum Conicarum, call number QA485 .S5 1735, can be found in the Linda Hall Library Digital Collections. In addition, the library has a 1750 Latin 2nd edition (call number QA485 .S5 1750) and a 1792 English 2nd edition, Elements of the Conic Sections (call number QA485 .S51 1792).

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Ackerberg-Hastings, Amy. "Mathematics is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790–1840." PhD diss., Iowa State University, 2000. DOI:10.31274/rtd-180813-13933.

Index to Mathematical Treasures

 

The above portrait is of Englishman Sir Samuel Morland from his 1673 book The Description and Use of Two Arithmetick Instruments, about two hand calculators and a perpetual almanac that Morland invented. Below is the title page.

The first of the two instruments described in this work carries out addition and subtraction of English currency (pounds, shillings, pence, and farthings). The images below show the first page of the section of the book about this instrument, the beginning of the instructions on how to use it, a drawing of its gear wheels, and an example.

The book then has the description of a second handheld instrument which carries out multiplication.

Sir Morland commented that, using the two instruments together, one could add, subtract, multiply, divide, and extract roots. He also mentioned “Lord Napiers Bones.”

The next section of the book contains a short history of numeration as well as exposition on arithmetic, including operations with decimals and fractions.

The image above appears in a section on extracting square roots and is based on the identity \( (a + b )^2 = a^2+ 2ab + b^2 \).

A complete digital scan of Morland’s Two Arithmetick Instruments, call number QA75.M64 1673, can be found in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Turner, G. L’E. "Morland, Samuel." In Complete Dictionary of Scientific Biography. New York: Charles Scribner's Sons, 2007. Encyclopedia.com. https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/morland-samuel (accessed 26 February 2018).

Index to Mathematical Treasures

The image below is the title page of De circulo et adscriptis liber, by the mathematician and fencing master Ludolph Van Ceulen (1540–1610). Originally published in Dutch in 1596 as Vanden Circkel, De Circulo is a modified version that Van Ceulen's student Willebrord Snell (1580–1626) translated into Latin in 1619 to make it more accessible.

The engraving on the title page is the same one used for the Dutch original. Notice that below the portrait of Van Ceulen is a circle with diameter of \(10^{20}\). Along the top and bottom semicircles is printed “314159265358979323846 te cort” (too short) and “314159265358979323847 te lanck” (too long). These bounds for \(\pi\) were the best ones available when Vanden Circkel was published in 1596. Later, Van Ceulen determined \(\pi\) to 35 decimal places. As evidence of the importance of Van Ceulen’s work, \(\pi\) has been known as “Ludolph’s number” or the “Ludolphine number”, especially in Germany and the Netherlands. For example, when Ferdinand von Lindemann published his proof of the transcendence of \(\pi\) in 1882, although he used the Greek letter \(\pi\), he also used the term “Ludolph’sche Zahl”. (See “Ueber die Zahl \(\pi\)” 1882, in the middle of page 223.) Even Euler, in a 1743 paper, writes, “It is clear that I employ here the letter \(\pi\) to denote the number of Ludolf van Ceulen 3.14159265 ··· .” (See Lagarias 2013, on page 544.)

Van Ceulen’s work with \(\pi\) was greatly aided when an acquaintance translated from Greek Archimedes’ method using inscribed and circumscribed regular polygons. Below is an image of page 2 of De Circulo showing a regular hexagon inscribed in a circle being used to then inscribe a regular dodecagon.

Images from pages 3, 12, and 17 follow. On page 3 is a result relating a rectangle to a square which are inscribed in circles with different diameters. Page 12 starts a chapter dealing with irrational numbers. The notation \(\sqrt{.2}-\sqrt{3}\) is used for \(\sqrt{2-\sqrt{3}}\). Chapter 7 begins on page 17 with an equilateral triangle and a regular hexagon inscribed in a circle.

Below on page 5, starting with a square inscribed in a circle with diameter 2, is a sequence of line segments constructed with increasing lengths \(\sqrt{2+\sqrt{2}}\), \(\sqrt{2+\sqrt{2+\sqrt{2}}}\), …

On page 48 below, a table with the length of a side of a regular polygon is inscribed in a circle with radius 200,000,000,000, where the number of sides ranges from 3 to 80. There is at least one typographical error; the first digit for a polygon with 4 sides should be 1, not 2. Below the table is a note giving glory to God for leading Van Ceulen through the work.

On the next page we see N used for a side, Q and a script Q used for square, C for cube, QQ for quartic, QC for quintic, etc.

More images from De Circulo are available on Convergence. Images from the 1594 Dutch original Vanden Circkel are also available here.

A complete digital scan of De Circulo is available in the Linda Hall Library Digital Collections. The call number is QA33 .C481 1619.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Acknowledgements

Thanks are due to Dominic Klyve, Jeffrey Lagarias, Chuck Lindsey, and Heiko Todt for providing examples of places where the term “Ludolph’s number” appears.

References

Lagarias, J. C. “Euler's constant: Euler's work and modern developments,” Bull. Amer. Math. Soc. 50, no. 4 (2013): 527–628.

“Ueber die Zahl \(\pi\),” Mathematische Annalen 20 (1882): 213–225.

Index to Mathematical Treasures

Surdorum quadraticorum arithmetica (Arithmetic of Square Roots) is a work by the mathematician and fencing master Ludolph Van Ceulen (1540–1610), which was translated into Latin by his student Willebrord Snell (1580–1626). It was published after the death of Van Ceulen, along with Snell’s modification and Latin translation De Circulo of Van Ceulen’s Vanden Circkel, which was published in 1596. Images from the 1594 Dutch original Vanden Circkel are available on Convergence. Images from De Circulo are available on Convergence here and here. The last two images in the first link above for De Circulo are actually from Surdorum quadraticorum arithmetica, which was bound together with De Circulo.

The opening page of Surdorum quadraticorum arithmetica is below.

Chapter 2 is about the addition of “simple irrational numbers”, that is square roots which when simplified have a common square root factor, such as \(5\sqrt{3}\) and \(2\sqrt{3}\). However Van Ceulen does not simplify irrational square roots like we do today; for example he uses \(\sqrt{75}\) rather than \(5\sqrt{3}\). Below are images of pages 4 and 5 showing several examples of his method for adding these simple irrational numbers.

Van Ceulen’s method for adding this type of square roots is to add together the sum of the radicands with the square root of the product of the radicands multiplied by 4. The solution is the square root of this sum. His example on page 4 is to find the sum \(\sqrt{75} + \sqrt{12}\). Notice \(75+12=87\) and \(75\times 12=900\). Then the square root of \(900\times 4= 3600\) is \(60\), and \(60+87=147\). So \(\sqrt{75} + \sqrt{12}=\sqrt{147}\). Additional examples are then given on page 5, pictured above.

Upon closer inspection of the addition examples, one notices that, if simplified, they are all of the form \(a\sqrt{c} + b\sqrt{c}=(a+b)\sqrt{c}\), where \(a, b, c\) are all positive integers. So, using Van Ceulen’s non-simplified notation, the sum is of the form \(\sqrt{a^2c} + \sqrt{b^2c}\). Four times the product of the radicands is then \(4a^2b^2c^2\) which is the square of \(2abc\). Adding \(2abc\) to the sum of the original radicands yields \(a^2c + 2abc + b^2c = (a+b)^2c\). Thus, his method produces the desired sum for this special case of irrationals, \(a\sqrt{c} + b\sqrt{c}=\sqrt{a^2c} + \sqrt{b^2c}= \sqrt{a^2c + 2abc + b^2c} = \sqrt{(a+b)^2c}=(a+b)\sqrt{c}\).

Below on page 85, is a figure of the Pythagorean Theorem applied to a 5–12–13 right triangle.

A complete digital scan of Surdorum quadraticorum arithmetica is available in the Linda Hall Library Digital Collections, starting after the scan of De Circulo, which is 54 pages long. The books are bound together and assigned the call number QA33 .C481 1619.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

 

The above image is the title page of Vanden Circkel, a book about the circle and \(\pi\) by Ludolph Van Ceulen (1540–1610). Published in 1596 in Dutch, it contains the longest decimal approximation of \(\pi\) at the time—20 decimal places. In fact, below the portrait of Van Ceulen, the engraving on the title page has a circle with diameter of \(10^{20}\). Across the top semicircle is “314159265358979323846 te cort” (too short), and “314159265358979323847 te lanck” (too long) is along the bottom semicircle. Later, Van Ceulen would determine \(\pi\) to 35 decimal places. A modified Latin version of the work was published in 1619, images of which can also be found on Convergence here and here.

Part of what little is known of Van Ceulen’s life before 1578 comes from the Preface of Vanden Circkel. Starting in 1566, he earned a living as a mathematics teacher, and in 1580 he opened his first fencing school. A few years later Archimedes’ method of approximating \(\pi\) was translated from the Greek for him, and Van Ceulen proceeded to use the technique to improve on approximations of \(\pi\), publishing Vanden Circkel in 1596. Below are images from folio 1 and folio 7.

Chapter 21 is devoted to analyzing a work of Joseph Justice Scaliger (1540–1609) called Cyclometrica Elementa (Elements of Circle Measurement), which had several incorrect results, including a “proof” that the area of a circle is equal to \(\frac{6}{5}\) of the area of an inscribed regular hexagon, which results in \(\pi = \frac{9}{5}\sqrt{3}\) or approximately 3.117691454. Van Ceulen doesn’t mention Scaliger by name, but rather calls him a “highly learned man”. Below is Folio 63a.

The subtitle translates as “Here follow some pieces in the art [of mathematics], concerning the circle, proposed and found by a highly learned man, in which [pieces] his illustrious mind is evident. These pieces have been sent to me and he desires to have my opinion of them. Therefore I have answered them by investigating them, and I have found most of them to be correct by means of numbers.” [Hogendijk, p. 349] (The article by Hogendijk contains an English translation of Chapter 21.)

A complete digital scan of Van Ceulen’s Vanden Circkel, call number QA33 .C48 1596, can be found in the Linda Hall Library Digital Collections.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Reference

Hogendijk, Jan P. "The scholar and the fencing master: The exchanges between Joseph Justus Scaliger and Ludolph van Ceulen on the circle quadrature (1594–1596)." Historia Mathematica 37 (2010): 345–375.

Index to Mathematical Treasures

Famous as an Enlightenment philosopher, poet, and writer, Voltaire also studied science and mathematics, including works by Newton. His interest in these topics may have been influenced by his mistress Émilie du Châtelet, who later was known for her translation and commentary of Newton’s Principia. (For images of her translation and commentary, visit the page Mathematical Treasure: Émilie du Châtelet’s Principes Mathématiques.) Voltaire’s work, Élémens de la philosophie de Neuton : mis à la portée de tout le monde, was first published in 1738 in French in Amsterdam. An Italian version was published in 1741, and a revised French edition in 1773 (about five years before the death of Voltaire). This book contributed to the spread of Newton’s ideas on gravity, optics, and light to France, by making them more understandable and accessible. Below is an image of the title page from the 1738 edition.

Notice that the title page lists Voltaire’s name as the sole author. There is speculation that if the book had been written in a different culture and age that Émilie du Châtelet would have been listed as a co-author. Preceding the title page, there is a portrait of Voltaire and a scene depicting Voltaire writing at a table. He is receiving inspiration from a beautiful goddess (Émilie) who is holding a mirror that reflects ideas down from Newton in the clouds. Images of these two frontispiece pages are below.

Voltaire explicitly gave credit to Émilie du Châtelet in an acknowledgment and foreword. Images of the first page of each of these are below.

The next images are from a discussion of the angles involved when a ray of light passes through a crystal and how white light is broken up into colors when it passes through a prism.

Émilie du Châtelet wrote a review of Voltaire’s Élémens de la philosophie de Neuton which appeared in the September 1738 issue of the Journal des Sçavans under the heading “De Cirey en Champagne”. Voltaire and Émilie spent many years together at her estate called Cirey, conducting experiments, reading, writing, and hosting other researchers. Three years later, in 1741, she published a book synthesizing the ideas of Descartes, Leibniz, and Newton. Images from this work can be found on the page Mathematical Treasure: Émilie du Châtelet’s Institutions de Physique.

The call number for the 1738 French edition of Voltaire’s Elements of the Philosophy of Newton is QC19.V64 1738.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Arianrhod, Robyn. Seduced by Logic: Émilie du Châtelet, Mary Somerville, and the Newtonian Revolution. Oxford, 2012.

Bodanis, David. Passionate Minds: The great love affair of the Enlightenment, featuring the scientist Emilie du Châtelet, the poet Voltaire, sword fights, book burnings, assorted kings, seditious verse, and the birth of the modern world. Crown Publishers, 2006.

Zinsser, Judith P. Emilie du Chatelet: Daring Genius of the Enlightenment. Penguin Books, 2006.

Index to Mathematical Treasures

 

The above image is the title page of Elementi Decimi Euclidis Declaratio (A Clarification of the Tenth Book of Euclid’s Elements, 1662) by William Oughtred (1574–1660). Oughtred, an English clergyman and mathematician, is best known for inventing a slide rule and for his influential work Clavis Mathematicae. Images of a 1631 Latin edition, a 1667 Latin edition, and a 1647 English translation of Oughtred’s Clavis Mathematicae are available on Convergence.

The next two images show the notation used in Oughtred’s work on Euclid, starting off with symbols for equal, greater than, and less than.

The image below is page 5, containing a section of lemmas. With the help of the notation guide (the last two lines of the first page and the first two lines of the second page), one can see that the second lemma shows the expansion of binomials, \(A^2 + E^2 – 2AE = (A-E)^2\) and \(A^2 + E^2 + 2AE = (A+E)^2\).

There is also a section on the five regular solids which includes nets for all but the icosahedron.

A complete digital scan of Oughtred’s 1662 Elementi Decimi Euclidis Declaratio can be found in the Linda Hall Library Digital Collections. It is bound together with a 1667 edition of Oughtred’s Clavis Mathematicae, call number QA33 .O73 1667, and two of Oughtred’s other works, Theorematum in Libris Archimedis de Sphaera & Cylindro Declaratio (1663) and Horologiorum Sciotericorum in Plano (1663).

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

William Oughtred (1574–1660) was an English clergyman and mathematician. He tutored several well-known people, including John Pell, John Wallis, and Christopher Wren, and his influential work Clavis Mathematicae was used by Isaac Newton. Images of a 1631 Latin edition, a 1667 Latin edition, and a 1647 English translation of Oughtred’s Clavis Mathematicae are available on Convergence.

Oughtred also wrote other works, including a 10-page treatise called Theorematum in Libris Archimedis de Sphaera & Cylindro Declaratio, translated as A Clarification of Theorems in Archimedes’ Books on the Sphere and the Cylinder. Below is the title page, which has the date 1663.

The next image shows the second page, titled “Rerum quarundam denotations” or “Notations of Certain Things,” which lists notation used in the work.

Oughtred was known for his innovative use of symbols. In the first item in the page above, he uses R for the radius or semidiameter of a circle; in later entries a delta-like symbol is used for diameter and \(\pi\) is used for the circumference of a circle. In the second entry, using a dot or period for ratio and a double colon for proportion, he states that the ratio of the diameter to the circumference is in proportion with the ratio of the semidiameter (radius) to the semiperimeter (half the circumference). The fifth entry gives the area of the circle as circumference divided by diameter times the radius squared.

The image above shows the start of the exposition. It contains the first two theorems from Archimedes’ On the Sphere and the Cylinder. Oughtred goes on to state twenty more theorems dealing with cones, spheres and cylinders.

A complete digital scan of Oughtred’s 1663 Theorematum Archimedis (starting on page 221) can be found in the Linda Hall Library Digital Collections. It is bound together with three other works by Oughtred: a 1667 edition of Clavis Mathematicae, call number QA33 .O73 1667; Elementi decimi Euclidis Declaratio [Euclid’s Ten Elements Clarified] (1662); and Horologiorum Sciotericorum in Plano (1663).

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

Index to Mathematical Treasures

Best known for her translation of and commentary on Newton’s Principia, Émilie du Châtelet, also published other works. Born Gabrielle-Émilie Le Tonnelier de Breteuil, married to the Marquise du Chastellet, and mistress of the French poet Voltaire, Émilie was a mathematician and scientist in France during the Enlightenment. The following image is the title page of a revised French edition of Émilie du Châtelet’s Institutions de Physique, published in 1741 in Holland. The first edition was published the previous year, and several other editions followed. Émilie wrote this book, in which she assimilated points of view of Descartes, Newton, and Leibniz, to teach new ideas in physics to her thirteen-year-old son. Notice that her name is not mentioned on the title page of this edition. There was a 1742 edition also published in Amsterdam which was not anonymous.

The frontispiece is interesting. It shows a person (possibly du Châtelet) climbing to reach a glorious temple occupied by “Truth” depicted as a naked woman. Cherubs hold portraits at the top of the page, possibly representing Descartes, Leibniz, and Newton.

Each chapter begins with a delightful graphic exhibiting mathematics or science in some way. For example, Chapter 14 on the phenomena of gravity has a picture of a device used to demonstrate Galileo’s law of natural motion. The paraboloid apparatus involves dropping balls on a spiral track to show that each turn of the spiral is traveled in the same amount of time (isochronism).

According to the virtual Galileo Museum, there are only two such devices currently known to be in existence. The picture below is at the Galileo Museum in Florence, Italy, taken by the author while on the 2012 MAA Study Tour.

In her biography of Émilie du Châtelet, Judith P. Zinsser questions whether these chapter opening graphics tie in with the fact that Émilie wrote the book to teach her son the fundamentals of physics, since “many of the decorative illustrations at the beginnings of the Institutions’s chapters show a young boy at games and activities demonstrating one or the other law of motion: lacrosse, billiards, balancing on a seesaw, shuttlecock, riding, shooting a gun.” (Zinsser, p. 165) Images of several of these illustrations follow.

    

    

   

The call number for the revised 1741 French edition of Émilie du Châtelet’s Institutions de Physique is QC19.D85 1741. A digital copy is available in the Linda Hall Library Digital Collections.

Except for the image of the apparatus at the Galileo Museum in Florence which was taken by the author, all other images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

For a portrait of Émilie du Châtelet, visit the Francesco Algarotti page of Mathematical Treasures.

References

Bodanis, David. Passionate Minds: The great love affair of the Enlightenment, featuring the scientist Emilie du Châtelet, the poet Voltaire, sword fights, book burnings, assorted kings, seditious verse, and the birth of the modern world. Crown Publishers, 2006.

“Gabrielle Émilie Le Tonnelier de Breteuil Marquise du Châtelet.” MacTutor History of Mathematics Archive. http://www-history.mcs.st-and.ac.uk/Biographies/Chatelet.html.

Taton, René. “Châtelet, Gabrielle-Émilie Le Tonnelier de Breteuil, Marquise du.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, iii:215–217. New York: Scribner, 1972.

Virtual Galileo Museum. “Apparatus to demonstrate the isochronism of falls along a spiral.” http://catalogue.museogalileo.it/object/ApparatusToDemonstrateIsochronismFallsAlongSpiral.html.

Zinsser, Judith P. Emilie du Chatelet: Daring Genius of the Enlightenment. Penguin Books, 2006.

Index to Mathematical Treasures

Émilie du Châtelet, born Gabrielle-Émilie Le Tonnelier de Breteuil, married to the Marquise du Chastellet, and mistress of Voltaire, was a mathematician and scientist in France during the Enlightenment. The following image is the title page of volume 1 of Émilie du Châtelet’s Principes Mathématiques de la Philosophie Naturelle, a two-volume translation and commentary of Newton’s Principia, published in 1759 in French in Paris. It is considered her greatest achievement. The complete work appeared ten years after her death, and it still is the only complete French translation available. According to the Dictionary of Scientific Biography, “her work contributed to the great progress made by Newtonian science in the middle of the eighteenth century.”

Page one of volume 1 begins with Definitions.

Lemma 1 (page 37) is related to the notion of a limit and roughly translated states that if two quantities are tending towards being equal in such a way that their difference can be found to be less than any given difference, then the quantities are equal.

This is followed by Lemma 2 (page 38 and Figure 6 on a foldout after page 82), using inscribed and circumscribed parallelograms (rectangles) to find the area under a curve.

Du Châtelet used Leibniz’s notation for differentials and integrals as demonstrated on page 129 of Volume 2.

Complete digital scans of Principes Mathématiques de la Philosophie Naturelle, Volume 1 and Volume 2, are available in the Linda Hall Library Digital Collections. The call number is QA803.A53 1759. For a portrait of Émilie du Châtelet, visit the Francesco Algarotti page Mathematical Treasures.

Several books have been written about the life of Émilie du Châtelet, including Passionate Minds: The great love affair of the Enlightenment, featuring the scientist Emilie du Châtelet, the poet Voltaire, sword fights, book burnings, assorted kings, seditious verse, and the birth of the modern world by David Bodanis, which reads like a novel and contains many details gleaned from letters written by Emilie and Voltaire and their acquaintances. According to Bodanis, “her translation and commentary on Newton’s Principia became fundamental to key eighteenth-century developments in theoretical physics, laying the groundwork for much of contemporary science. … More technical aspects of her work played a great role in energizing the French school of theoretical physics, associated with Lagrange and Laplace." (pp. 281, 283)

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Bodanis, David. Passionate Minds: The great love affair of the Enlightenment, featuring the scientist Emilie du Châtelet, the poet Voltaire, sword fights, book burnings, assorted kings, seditious verse, and the birth of the modern world. Crown Publishers, 2006.

O'Connor, J. J., and E. F. Robertson. “Gabrielle Émilie Le Tonnelier de Breteuil Marquise du Châtelet.” MacTutor History of Mathematics Archive. http://www-history.mcs.st-and.ac.uk/Biographies/Chatelet.html.

Taton, René. “Châtelet, Gabrielle-Émilie Le Tonnelier de Breteuil, Marquise du.” In Dictionary of Scientific Biography, edited by C. C. Gillespie, iii:215–217. New York: Scribner, 1972.

Index to Mathematical Treasures