Mathematical Treasure: Harriot’s Artis Analyticae Praxis

Written by Thomas Harriot, Artis Analyticae Praxis (Practice of the Art of Analysis) was published in 1631, ten years after Harriot’s death. According to Katz and Parshall, “a convert to Viète’s ideas, the Englishman [Harriot] extended them by making algebraic arguments even more symbolic. ... Harriot’s notational innovations made Viète’s ideas an even more useful tool for manipulating and solving equations. [Then] Fermat … fashioned these ideas into a tool for dealing algebraically with curves in the plane.” (Katz & Parshall, pp. 249, 252) Below is the title page of Artis Analyticae Praxis.

Next are images of three pages with examples of arithmetic operations using variables.

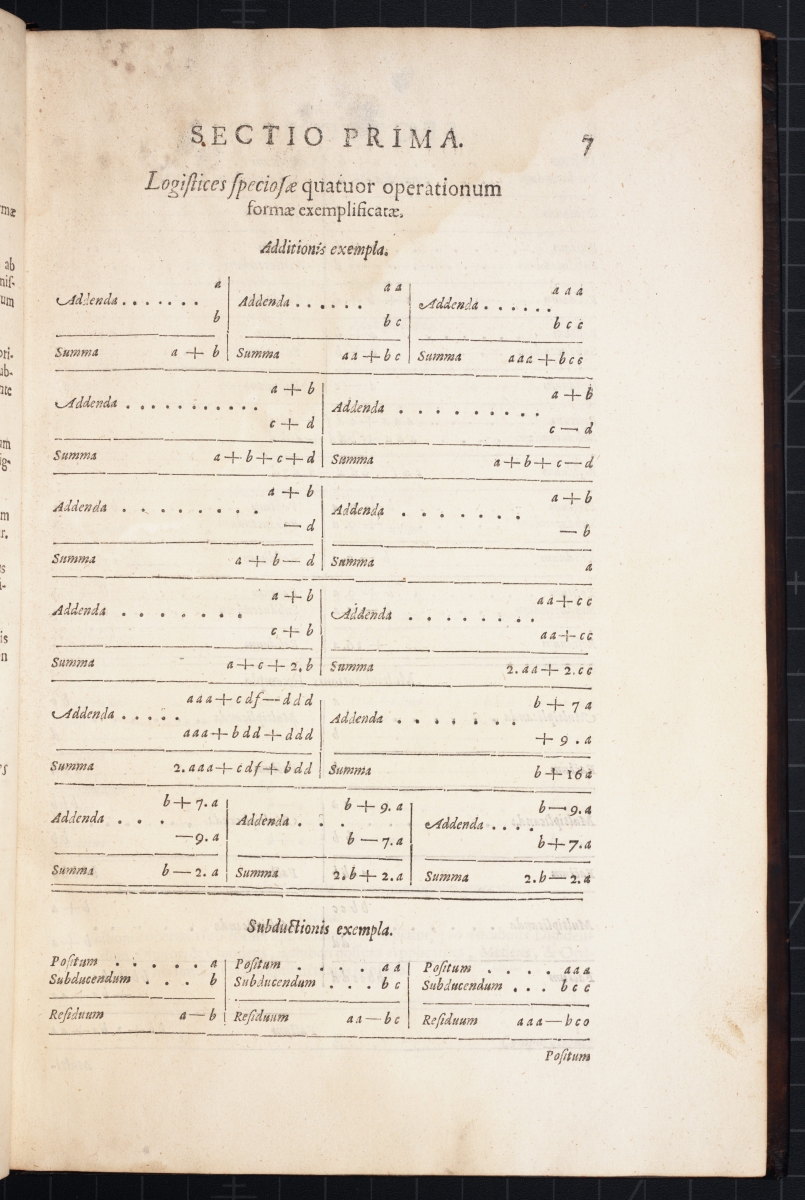
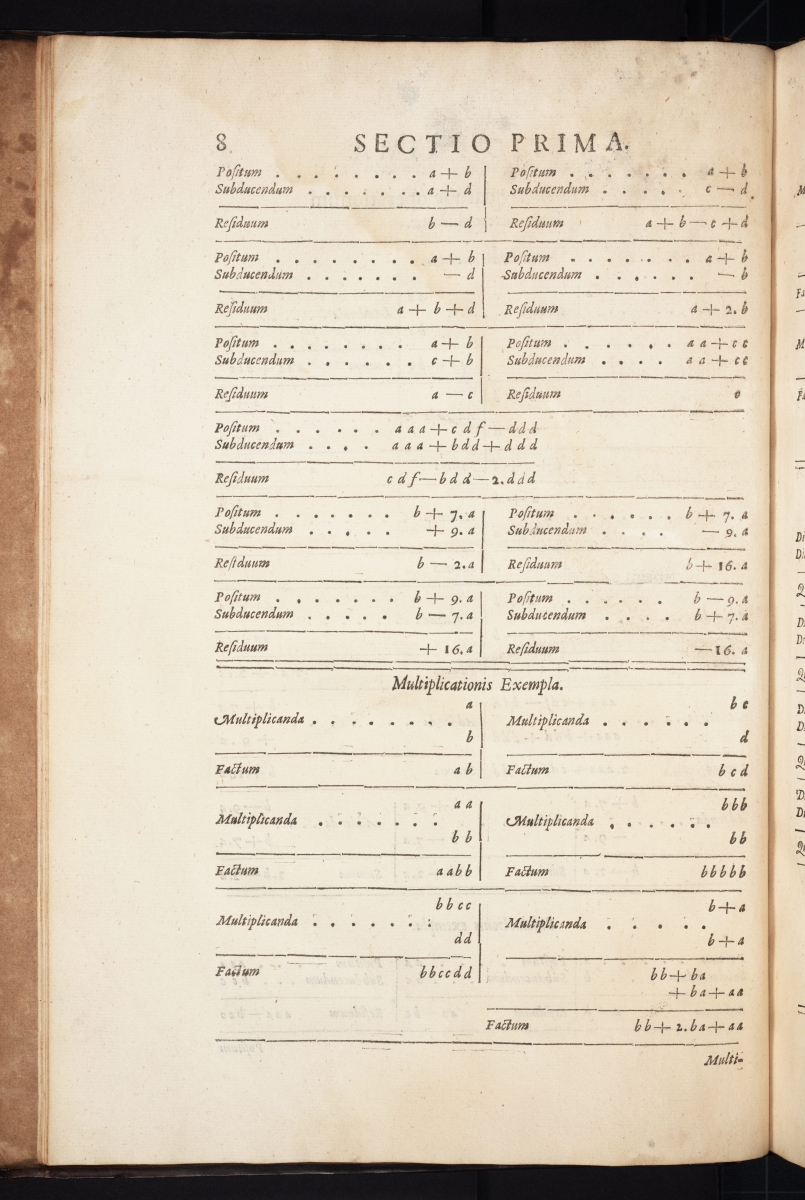
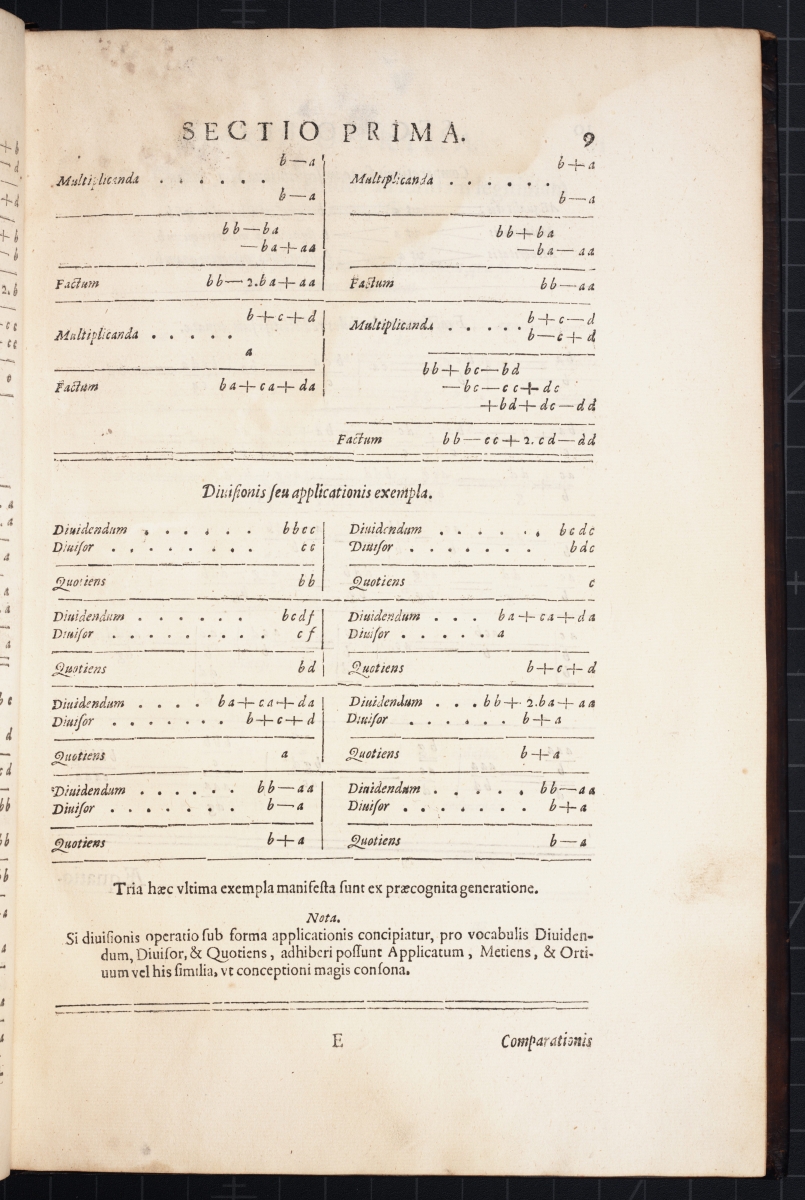
The image below shows the derivation of the quadratic equation \( a^2 – ba + ca = bc \) from expanding \( (a – b)(a + c) = 0 \).

The image below shows reducing the trinomial \( a^3 – 3ba^2 + 3b^2a = b^3 + c^3 \) to the binomial \( a^3 – 3bca = b^3 + c^3 \).

Images from another copy of the 1631 edition of Artis Analyticae Praxis can also be found in Convergence.

English translations of Harriot’s Artis Analyticae Praxis are available on the web and in print.

A complete digital scan of Artis Analyticae Praxis is available in the Linda Hall Library Digital Collections. The call number is QA33.H37 1631.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The images may be downloaded and used for the purposes of research, teaching, and private study, provided the Linda Hall Library of Science, Engineering & Technology is credited as the source. For other uses, check out the LHL Image Rights and Reproductions policy.

Reference

Katz, Victor J., and Karen Hunger Parshall. Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century. Princeton: Princeton University Press, 2014.

Index to Mathematical Treasures