Thinking Outside the Box -- or Maybe Just About the Box

Background

Historical References

The Box problem is so timeless that it even goes back almost a hundred years to the classic Granville and Smith (1911) text. Except for the fact that it is made out of tin, doesn't this look familiar?

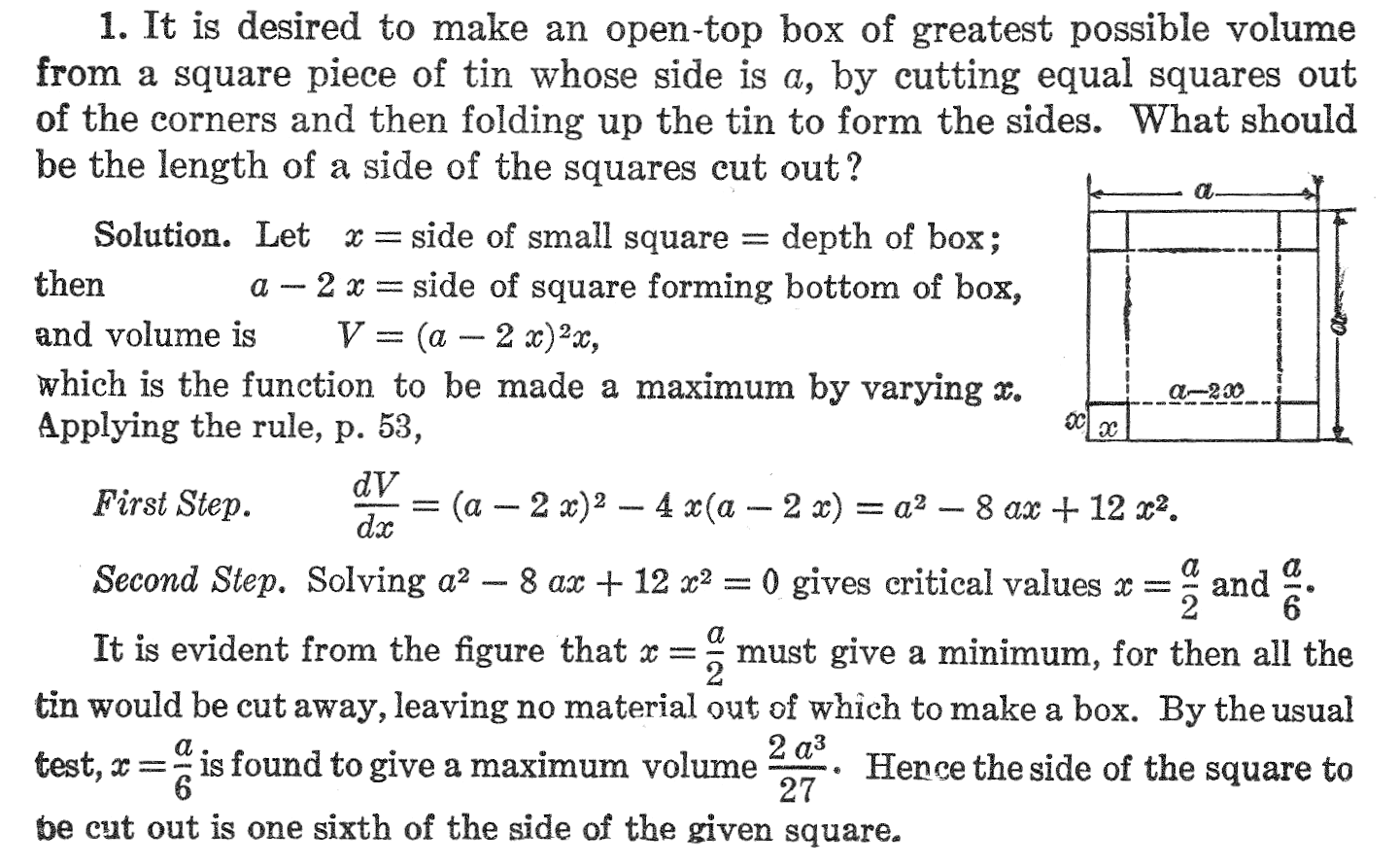Figure 2. The box problem on page 115 in Granville and Smith (1911)

However, this instance was not the first appearance of the box problem in either an academic publication or in popular culture. A derivation of the box problem first appeared in popular culture in the 1903 Henry Dudeney's puzzle column in the Weekly Dispatch and again in 1908, it was rephrased for his puzzle column in Cassell's Magazine. Below is the graphic and phrasing of the problem contained in Cassell's Magazine:

Figure 3. Illustration from Cassell's Magazine.

''No. 525 -- HOW TO MAKE CISTERNS. Here is a little puzzle that will elucidate a point of considerable importance to cistern makers, ironmongers, plumbers, cardboard-box makers, and the public generally.

Our friend the cistern-maker has an interesting task before him. He has a large sheet of zinc, measuring eight feet by three feet, and he proposes to cut out square pieces from the four corners (all, of course, of the same size), then fold up the sides, join them with solder, and make a cistern.

So far, the work appears to be pretty obvious and easy. But the point that puzzles him is this: What is the exact size for the square pieces that he must cut out if the cistern is to contain the greatest possible quantity of water?

Call the feet inches, and take a piece of cardboard or paper eight inches long and three inches wide. By experimenting with this you will soon see that a great deal depends on the size of those squares. To get the greatest contents you have to avoid cutting those squares too small on the one hand and too large on the other. How are you going to get at the right dimensions? I shall award our weekly half-guinea prize for a correct answer. State the dimensions of the squares and try to find a rule that the intelligent working man may understand.''

(Dudeney, 1908, p. 430)

But just in case one might think that the problem is only a century old, a Treatise on Differential Calculus by Todhunter (1855) contains the following related problem:

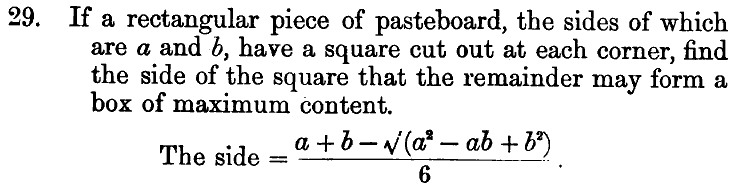
Figure 4. The box problem on page 213 of Todhunter (1855).

Consequently, this problem has appeared in calculus texts for at least the last one and a half centuries. It has become so entrenched in the calculus curriculum and articles are still being written about it. For instance, an article by Miller and Shaw (2007) breathed new life into this problem for it served as the backdrop to explore a conventional problem in unconventional ways or an article by Fredrickson (2003) reconceptualizing the constraints on the ''cutouts'' while striving for a container of maximum volume. But what is it about this problem that makes it so universal and mathematics teachers keep coming back to it? Does it really motivate student learning of essential calculus concepts? We concur with Underwood Dudley (2002) when he pointed out in his talk on Calculus Books, "when have you encountered a cardboard box constructed in such a way?" and the problem is ''quite silly'' according to Friedlander and Wilker (1980), Dundas (1984) and Pirich (1996) since the corners are wasted.

As previously identified, this particular calculus problem predates modern use of cardboard packaging. But, most would agree that constructing a cardboard box in this manner is quite unusual. So, why do calculus teachers keep including it as part of their repertoire of examples other than the fact that it is straightforward and easily comprehensible? Doesn't the inclusion make students begin to wonder about the ability of calculus to model reality? In fact, if one attempts to rip apart the classic open box used for the typical shirt box that one receives at Christmas, it is not constructed in this manner.

It is interesting to note that both the Granville and Smith text and Dudeney's puzzle used tin, a little more practical material than cardboard for such a construction. A box of cardboard might use the squares as tabs to connect the sides together and increase stability and strength. In fact, we have often asked students to construct boxes from index cards we gave them and they tend to do use these tabs naturally to make the connections with tape, glue or a staple. The students can typically answer the mathematical questions of the corner-removed box problem but at the same time they recognize the lack of realism when the corners are removed since boxes just are not constructed that way.