Virginia State University

Title: Geometric Properties of the Apollonian Circle Packing

Director: Dawit Haile & Raymond Fletcher

Email: dhaile@vsu.edu & rfletcher@vsu.edu

Dates of Program: May 15 - June 24, 2008

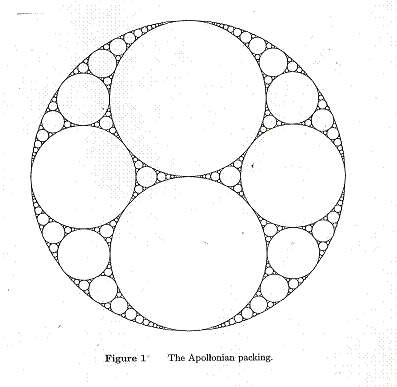
Summary: The Apollonian circle packing (Figure 1) provides a rich setting for geometric research. The mutually tangent circles A, B, C and the inner and outer Soddy circles O₁, O₂ form the basis for the Apollonian packing; the remainder of the packing is obtained by repeatedly inserting circles tangent to three circles in the system. It is known that the Soddy line O₁O₂ contains the incenter I and the Gergonne point G of triangle ABC. In this research project, we will attempt to demonstrate the existence of an infinite number of points which also lie on the Soddy line and which arise as concurrence points of lines which join contact points and/or center points of the packing. The points S and W in Figure 2 represent two such points.

As it turns out, the theory of midcircles and inversion is essential for understanding properties exhibited by the packing. Students participating in the research project will construct the midcircle(s) for two given circles ’, ’, prove their constructions, develop useful properties of midcircles and show how midcircles can be used to construct the packing. Geometers Sketch Pad will be used for the constructions and also to probe for new properties. An analytic approach using Mathematica will be used for problems not amenable to classical arguments.