- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Geometry from Africa: Mathematical and Educational Explorations

Buy Now:
Publisher:
Mathematical Association of America
Publication Date:
1999
Number of Pages:
150
Format:
Paperback
Series:
Classroom Resource Materials
Price:
48.50
ISBN:
978-0-88385-715-1
Category:
General
[Reviewed by , on ]
Karen Dee Michalowicz
10/12/1999
For those of us who hate to augment our libraries with softbound books, the MAA has come along with a good way to appease us. Geometry from Africa, like the book on Euler recently released by MAA, is beautifully printed with an extremely attractive cover. This work by Paulus Gerdes of the Universidade Pedagogica in Mozambique is a masterpiece. Not only are the illustrations within the Gerdes book plentiful, they have been well chosen so as to draw the reader into the mathematics of the artifacts and geometric figures.
Although there are other books and journal articles on connections between African artifacts and mathematics, there has not yet been a book in English which unites the Geometric patterns and thought of Africa with the related mathematics. There has also been nothing so useful for student investigations and research on Sub-Saharan African mathematics. The mathematics educator will be pleased. Furthermore, Gerdes' book leads the reader to understand that Africa is a "vibrant cultural mosaic." There are many different peoples with a great diversity in cultural and social mores, leading to many different expressions of mathematical design. This book challenges its readers to open their eyes to a large continent where hundreds of languages are spoken, where people are urban and rural, where there are many different countries with varied cultures, and where geometry lives in each groups everyday life. This book will likely be an eye-opener for many that think of Africa as a continent where everyone looks and lives alike and shares the same language.
The chapters in the book move from the geometrical ideas of Sub-Saharan Africa to discovering the Pythagorean Theorem in African designs, and then to exploring the geometric ideas in African crafts. Finally the sona sand drawing tradition is considered with a discussion of the possibilities for its educational use. Each chapter includes an extensive bibliography.
 In Chapter One, the reader is introduced to many different geometric designs that have been found in African artifacts for the past 2400 years. Of particular interest are the designs on the well-preserved Tellem textiles discovered in the Republic of Mali. The Tellem inhabited the area from about the 11th century until the 15th century CE. In analyzing the mathematics of the Tellem weaving, it immediately becomes apparent that the Tellem weavers understood patterns and the necessary relationship between dimension and symmetry in order to create them. It is amazing that they were able to create such intricate patterns using only white and indigo cotton threads, approximately 1mm thick. The first chapter also discusses the symmetry and patterns found in facial tattoos and hair design.
In Chapter One, the reader is introduced to many different geometric designs that have been found in African artifacts for the past 2400 years. Of particular interest are the designs on the well-preserved Tellem textiles discovered in the Republic of Mali. The Tellem inhabited the area from about the 11th century until the 15th century CE. In analyzing the mathematics of the Tellem weaving, it immediately becomes apparent that the Tellem weavers understood patterns and the necessary relationship between dimension and symmetry in order to create them. It is amazing that they were able to create such intricate patterns using only white and indigo cotton threads, approximately 1mm thick. The first chapter also discusses the symmetry and patterns found in facial tattoos and hair design.
Chapter Two directs the reader to consider the variety of African design and artifacts that can be used in educational contexts to discover the Pythagorean Theorem and proofs. This is not to say that the Sub-Saharan peoples discovered the Pythagorean Theorem and proofs. However, looking at the designs one can't help but wonder about the mind of the ancient Mozambican or other artisan while he or she worked on Pythagorean-like patterns. What relationships did they discover? Whatever the answer, the educator can take the interesting designs pictured in Gerdes book and lead students to find the Pythagorean Theorem in the designs. These make for much more interesting geometry tasks than those found in textbooks. Gerdes also relates the Latin squares, magic squares, and modular arithmetic to design in African crafts.
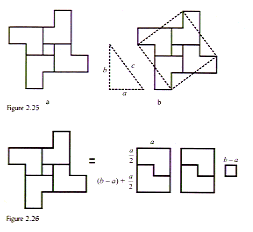 The Ngongo, for example, an ethnic group belonging to the Kuba kingdom, have a tattooing motif that can lead to the discovery of the Pythagorean Theorem. Gerdes mentions that mathematics historians have found these same patterns in ancient India and Chinese design. I plan to develop what Gerdes has presented using Ngongo tattoo design into a geo-board activity with my geometry students.
The Ngongo, for example, an ethnic group belonging to the Kuba kingdom, have a tattooing motif that can lead to the discovery of the Pythagorean Theorem. Gerdes mentions that mathematics historians have found these same patterns in ancient India and Chinese design. I plan to develop what Gerdes has presented using Ngongo tattoo design into a geo-board activity with my geometry students.
In Chapter Three the reader is presented with educational ideas about how to link geometry to African crafts. Artifacts from Congo/Zaire, Mozambique, Tanzania, Guinea, Senegal, Uganda, Cameroon, Kenya, Madagascar and the Lower Congo are used to help the educator to see how explorations of concepts related to symmetry, the pyramid, hexagons and pentagrams, and rectangle constructions to discover the areas of circles and volumes spatial figures can be used with students. This chapter is rich with ideas for student activities.
The final chapter looks at the sona sand drawing tradition among the Chokwe in southern-central Africa. Sona drawings were illustrations that went along with story telling. Certain drawings became traditional with certain stories. Some of the more difficult sona were know only by the storytellers. The techniques of these drawings were passed on to the storytellers male descendants. They were the elite in the Chokwe society. The slave trade caused the sona drawings to disappear. What we know of sona drawing comes mainly from 289 drawings collected by an ethnographer in the 1940s and 1950s.
 The sona used geometric algorithms to construct their drawings. They used a type of coordinate system with a grid (net) of points. The storytellers preferred designs that were simultaneously symmetrical and monolinear. Included in this chapter are ideas for the educator to use with students to look at arithmetical relationships and progressions, the geometrical determination of the GCF, the dimensions of rectangular grids, constructions of monolinear designs and their algorithms, polyhedral designs, etc.
The sona used geometric algorithms to construct their drawings. They used a type of coordinate system with a grid (net) of points. The storytellers preferred designs that were simultaneously symmetrical and monolinear. Included in this chapter are ideas for the educator to use with students to look at arithmetical relationships and progressions, the geometrical determination of the GCF, the dimensions of rectangular grids, constructions of monolinear designs and their algorithms, polyhedral designs, etc.
If this book had only been designed for leading the reader to discover or connect mathematics in Sub-Saharan African artifacts, it would still be much valued. However, because the book is also an educational resource for teachers, it is my opinion that every mathematics educator would benefit from having access to this book for work with students. I have bought two, one for my schools mathematics library and one for my own bookshelf.
In conclusion, I must admit that some will look at the Gerdes book and say that the mathematics is contrived. Until we see and thus lead our students to see and understand mathematics as broader than academic mathematics, we will not appreciate mathematics for what it really is. Does one need to study in a textbook the Pythagorean Theorem to understand it? Does one need to study coordinate geometry to draw symmetric, monolinear designs? I believe that connecting the academic mathematics with the African design, as Gerdes has, may lead the student to wonder in awe about the mathematics of the artisans of Africa!
Karen Dee Michalowicz (KarenDM@aol.com is Upper School Mathematics Chair at the Langley School in McLean, VA, and teaches "Multicultural Mathematics Methods K-8" in the FASTRAIN Program of the George Mason University Graduate School in Fairfax, VA. Her collection of old textbooks now contains over 500 books published between 1529 and l899.
See the table of contents in pdf format.
- Log in to post comments




