- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Math Made Visual: Creating Images for Understanding Mathematics

Publisher:
Mathematical Association of America
Publication Date:
2006
Number of Pages:
172
Format:
Hardcover
Series:
Classroom Resource Materials
Price:
49.95
ISBN:
0883857464
Category:
Monograph
The Basic Library List Committee recommends this book for acquisition by undergraduate mathematics libraries.
[Reviewed by , on ]
Richard J. Wilders
03/31/2011
This wonderful book is a fitting edition to the Classroom Resource series. Indeed any teacher of mathematics at the high school level or above should have a copy. Let me take that a bit further: anyone with an interest in mathematics should have a copy! While I ended up reading it pretty much straight through, this is a wonderful reference book which can be consulted whenever one is stuck for a way to make a concept come to life or for an activity to get students involved in mathematics.
The first two-thirds of the text consists of a wonderful set of examples of how visualization can aid understanding and inspire exploration. Each section ends with a set of challenges for the reader. These problems would make wonderful projects for pre-service high school teachers — many of them can be implemented in Geometer’s Sketchpad. The final section of the book consists of hints for solving these challenges. Sandwiched between these two sections is a short section providing suggestions as to how these ideas can be used on a classroom. While technology would certainly help, many of the hints involve simple paper folding and cutting. Geometer's Sketchpad would certainly suffice to create most all of the 2-dimensional figures.
Part I consists of 20 short chapters each with several related concepts. These chapters are only loosely related to one another and assume minimal mathematical background on the part of the reader. They seem designed with browsing in mind. If you are stuck for a way to explain a concept or for nice examples spend a few minutes with Math Made Visual. Here are a few samples. I am not going to attempt a summary as the book has no ‘plot’ — just a wonderful collection of short stories!
Chapters 1 through 4 demonstrate ways to represent numbers (and their sums and products) using geometric elements (triangular numbers), line segments, areas, and finally volumes. The formula 1 + 2 + … + n = n(n+1)/2 is derived in several interesting ways, all of them, I suspect, more convincing to students than the standard proof by induction. This formula and others (sum of the odd numbers, sum of the first n squares, etc) are then illustrated using line segments, areas, and volumes in subsequent chapters.
As one might expect, the Pythagorean Theorem shows up early and often. There is also a very nice proof of Herron's formula for the area of a triangle. We also encounter proofs of several of the standard trigonometric identities including Ptolemy's Theorem.
Chapter 14, Moving Frames, provides some very clever techniques to illustrate such ideas as functional composition, uniform continuity, the Lipschitz Condition and others.
There are some very clever inequalities lurking in here as well. For example, which is larger πe or eπ? This is perhaps the most interesting example of a general result: if e ≤ a < b, then ab > ba. Here is a sketch with all the information you need.
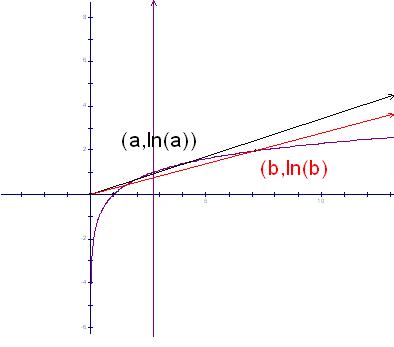
(Need a hint? See page 11)
In Chapter 8 on Area-Preserving Transformations we meet the ancient Greek problem of computing area by constructing a square of area equal to the area of the figure under study. The classic example here is squaring the circle which we now know to be impossible. It is easy to square a rectangle using the geometric mean and hence it is also possible to square a triangle. On page 35 we encounter the general result — a method which for any convex polygon with n sides constructs with straightedge and compass a convex polygon with n–1 sides with the same area as the original polygon.
One last example from page 91: ‘Take a piece of paper and scissors. Can you cut a hole in the paper large enough to walk through?’ The answer, as you might have guessed is yes. Fold the paper in half and make a series of cuts (nearly the entire folded width) alternating from the folded and unfolded side.
A review of this sort can't do this book justice. To appreciate it you have to see it. The visuals (and the wonderfully clear text which accompanies them) are wonderfully conceived and masterfully executed. This is a book you will find yourself picking up again and again.
Richard Wilders is Marie and Bernice Gantzert Professor in the Liberal Arts and Sciences and Professor of Mathematics at North Central College. His primary areas of interest are the history and philosophy of mathematics and of science. He has been a member of the Illinois Section of the Mathematical Association of America for 30 years and is a recipient of its Distinguished Service Award. His email address is rjwilders@noctrl.edu.
The table of contents is not available.
- Log in to post comments




