- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
On the Sector-Figure and Related Texts

Publisher:
Dr. Erwin Rauner Verlag
Publication Date:
2008
Number of Pages:
462
Format:
Paperback
Series:
Algorismus 67
Price:
38.50
ISBN:
9783936905311
Category:
Monograph
[Reviewed by , on ]
Glen Van Brummelen
01/26/2010
There are many reasons to study the history of mathematics; those most commonly expressed are its value in teaching and its ability to motivate mathematical interest in the population at large. But a crucial factor, often ignored, is the capacity of the history of mathematics to remind us that cultures shape mathematics in ways that can appear alien to us. The book under review is a scholarly study of two treatises by Thābit ibn Qurra, a ninth-century astronomer and mathematician. On the Sector-Figure deals with Menelaus’s Theorem, a fundamental result in ancient and medieval spherical astronomy. But where Thābit takes Menelaus in the second half of this work and the entire contents of the next, On the Composition of Ratios, will have modern readers feeling uncomfortable indeed.
Ancient and medieval mathematical astronomy took place mostly on the celestial sphere. The primary tool for determining magnitudes of arcs on this sphere was the following pair of theorems now named collectively after Menelaus, found at the beginning of Book III of his Sphaerica:
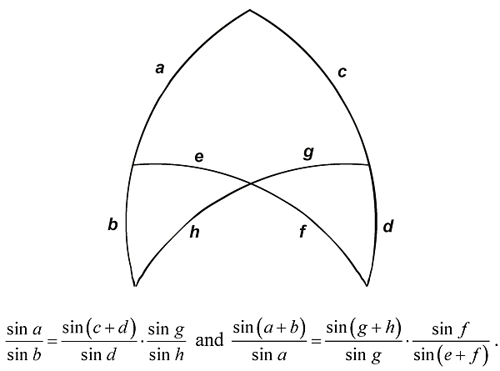
(To be precise, Menelaus used not the sine function but the ancient function called the chord; and trigonometric functions both in Menelaus’s and Thābit’s time were defined in terms of not the unit circle, but a circle of radius 60. We shall ignore such niceties here.) This seemingly awkward configuration was surprisingly useful for solving problems in spherical trigonometry, and it took until a century after Thābit before Menelaus was replaced by simpler theorems like the Rule of Four Quantities and the spherical Law of Sines.
So far this might seem a bit peculiar, but not exactly alien. However, after demonstrating the results, Thābit takes the subject in a direction that we would find rather odd. He takes the general form of both theorems, (a/b) = (c/d)(e/f), and considers what other ratios can be derived from it: for instance, (a/b) = (c/f)(e/d). He ends up with 18 different “modes” of the original expression, doubled to 36 if one inverts all the ratios in each equation. Now this seems like a rather trivial exercise; isn’t it just a matter of moving terms around the equation?
However, the ancient concept of ratio is different from ours. Our first sign of this is Lorch’s notation in his means of representing the expression, a:b = c:d ⊗ e:f. The colon signifies the fact that we aren’t in fractional Kansas anymore; the ⊗ indicates a “composition of ratios”, not a multiplication of fractions. In On the Sector-Figure Thābit quotes the Euclidean definition of ratio, “some relation of two homogeneous quantities among themselves in extent”. Lorch recounts the Euclidean approach to composition of ratios as dependent on these two statements:
- a:b ⊗ b:c is understood as a:c;
- If a:b = x:y and c:d = y:z then a:b ⊗ c:d = x:z.
If this is the logical basis of ratio theory, then one can’t just move terms in a ratio around an equality; one needs to prove each operation in turn. This is what takes up Thābit’s efforts in the rest of On the Sector-Figure. But in the last of the three chapters of On the Composition of Ratios Thābit changes his tune somewhat. Dealing with the problem of determining an unknown quantity within an equality of composed ratios when the other five are known, he eschews the Euclidean approach and adopts a more familiar arithmetical one. This is an important change of focus, one that could easily be missed by a modern reader.
Lorch’s book has three main parts. The first is an introduction to Thābit’s two treatises, his notions of ratio, and the manuscripts. The second, the bulk of the book, consists of Arabic editions and translations into English of both works, as well as editions of two medieval Latin translations of On the Sector-Figure. The third, “Towards a History of the Sector-Figure”, is a careful examination of a number of historical manuscripts related to Menelaus’s Theorem, tracing possible relations between them and to Thābit’s two works.
This book is written for scholars in the history of mathematics, not a general audience. Even so, it is a great service that it has been reprinted. Originally published in 2001 with a press run of only 50 (!), I was unable to find a copy in 2006 even at the institute where it had been published. Now it is more readily available, and I for one am very grateful that this detailed, impeccable study is now in wider circulation. But the interested mathematician or casual historian also might do well to struggle with at least some of its contents. To come to grips with a very different way of thinking about a familiar topic is to come a step closer to understanding the malleability of mathematical knowledge.
Glen Van Brummelen (gvb@questu.ca) is a historian of ancient and medieval mathematics and astronomy, and is the author of The Mathematics of the Heavens and the Earth: The Early History of Trigonometry (Princeton, 2009). His current book project is an attempt to bring spherical trigonometry back to the public imagination. Don Quixote would be proud.
I. Introduction — Thābit and the Sector-Figure
1. Thābit ibn Qurra
2. The Sector-Figure
3. Thābit’s Texts on the Sector-Figure and on the Composition of Ratios
4. Thābit’s Concept of Ratio
5. The Arabic Manuscripts
6. The Latin Translations of Thābit on the Sector-Figure
Appendix: The Hebrew Translation
7. Mathematical Notation
8. Editorial Principles and Conventions
II. Texts
1. Thābit’s Treatise, On the Sector-Figure, Arabic with English Translation
2. On the Sector-Figure, "Grecising" Latin Translation
3. On the Sector-Figure, Latin Translation, "Inter universas"
4. On the Sector-Figure, Mathematical Summary
5. Thābit’s Treatise, On the Composition of Ratios, Arabic with English Translation
6. On the Composition of Ratios, Mathematical Summary
III. Towards a History of the Sector-Figure
1. Earlier Redactions of Menelaus’ Spherica
Appendix: al-Māhānī’s Redaction; the D Redaction
2. Commentaries on the Almagest
Appendix: al-Nasawī and Desden Db 87; Almagestum parvum
3. Other Arabic Texts on the Sector-Figure
4. Applications of the Sector-Figure and of Alternative Theorems
6. The Sector-Figure and Related Material in Latin
Appendix: Further Latin Material
6. Campanus
Appendix: Campanus, De figura sectore
Bibliography
Index of Names
Index of Manuscripts
- Log in to post comments




