- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The College Mathematics Journal Contents—May 2010

Vol. 41, No. 3, pp. 182-260
Fermat's Last Theorem for Factional and Irrational Exponents
Frank Morgan
Fermat's Last Theorem says that for integers n > 2, there are no solutions to x n + y n = z n among positive integers. What about rational exponents? Irrational n? Negative n? See what an undergraduate senior seminar discovered.
Taylor's Theorem: The elusive c is not so elusive
Richard Kreminski
For a suitably nice, real-valued function f defined on an open interval containing [a,b], f(b) can be expressed as pn(b) (the nth Taylor polynomial of f centered at a) plus an error term of the (Lagrange) form f (n+1)(c)(b – a)(n+1)/(n+1)! for some c in (a,b). This article is for those who think that not much more can be said about where in (a,b) c is located. Supplementary materials, including further numerical illustrations and sketches of some proofs, are available at http://faculty.colostate-pueblo.edu/rick.kreminski.
When are Two Sets Congruent?
Jack Wetzel
The title question has at least two natural answers, one global and one local. Global: "when they can be made to coincide by a rigid motion of the whole plane;" local: "when there is a one-to-one distance preserving mapping of one onto the other." Self-evidently global implies local. We show that in fact these different notions lead to precisely the same notion of congruence.
Deranged Exams
Michael Spivey
This article discusses a triangle of numbers that are related to the derangement numbers. These numbers satisfy a Pascal-like recurrence relation with subtraction instead of addition. We describe how they relate to numbers studied by other authors and use them to generalize Euler's famous recurrence relation for the derangement numbers.
On Viviani's Theorem and its Extensions
Elias Abboud
Viviani's theorem states that the sum of distances from any point inside an equilateral triangle to its sides is constant. Here, in an extension of this result, we show, using linear programming, that any convex polygon can be divided into parallel line segments on which the sum of the distances to the sides of the polygon is constant.
Let us say that a polygon has the CVS property if the sum of distances from any inner point to its sides is constant. An amazing converse of Viviani's theorem is deduced: if just three non-collinear points inside a convex polygon have equal sums of distances then the polygon has the CVS property. For concave polygons the situation is quite different. For polyhedra analogous results are deduced.
Characterization of a Quadratic Function in Rn
Conway Xu
It is proved that a scalar-valued function f(x) defined in n-dimensional space must be quadratic, if the intersection of tangent planes at x1 and x2 always contains the midpoint of the line joining x1 and x2. This is the converse of a result of Stenlund proved in this JOURNAL in 2001.
Using Squares to Sum Squares
Duane DeTemple
Purely combinatorial proofs are given for the sum of squares formula,
 and the sum of sums of squares formula,
and the sum of sums of squares formula,

More precisely, the following algebraic equivalents are derived,
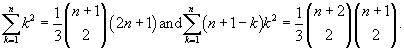
The proofs obtained literally count squares, namely lattice squares whose vertices are in an n x n grid. For the first formula, only lattice squares aligned to the grid are counted; for the second formula, aligned and tilted squares are counted.
The FedEx Problem
Kent Morrison
The original shipping strategy of FedEx was to fly all packages to a hub during the afternoon and evening, sort them there, and then fly them to their destinations over night for delivery the next day. This leads to interesting mathematical questions: Given a population represented by points in Euclidean space or on a sphere, what is the location of the hub that minimizes the total distance to all the points? Is such a point unique? After answering these questions, we use census data from 2000 to examine how close the FedEx hub in Memphis is to the proper hub of the U.S. population.
Three Poems
Nicole Yunger Halpern
CLASSROOM CAPSULES
Euler-Cauchy Using Undetermined Coefficients
By Doreen De Leon
The Euler-Cauchy equation is often the first higher order differential equation with variable coefficients introduced in an undergraduate differential equations course. Putting a non-homogeneous Euler-Cauchy equation on an exam in such a course, I was surprised when some of my students decided to apply the method of undetermined coefficients, supposedly guaranteed to work only for constant-coefficient equations, and obtained the correct answer! It turns out that a particular solution to this equation has a form similar to that of standard undetermined coefficients, if the right-hand side function is of a certain type. Thus the Euler-Cauchy equations can be solved without using variation of parameters or a substitution transforming the equation to a constant-coefficient equation.
Suspension Bridge Profiles
Charles Groetsch
The standard model of a uniform roadbed suspended from a weightless cable constrains the cable to a parabolic shape. What if the roadbed is not uniformly loaded? We characterize the shape of the suspension cable in this case, and show that, among other possibilities, a catenary may arise. Additional properties of such suspension profiles are discussed, and the work of a seventeenth century Jesuit savant makes a cameo appearance.
PROBLEMS AND SOLUTIONS
BOOK REVIEWS
MEDIA HIGHLIGHTS




