- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The College Mathematics Journal Contents September 2009
Vol. 40, No. 4, pp. 238-320
ARTICLES
Mechanical Circle-Squaring
Stan Wagon, Barry Cox
A technique discovered in 1939 can be used to build a device that is driven by standard circular motion (as in a drill press) and drills exact square holes. This device is quite different from the classic design by Watts, which uses a Reuleaux triangle and drills a hole that is almost, but not exactly, square. We describe the device in detail, deriving the equations needed to make a computer simulation. Then we investigate the extension to other polygons and show how the basic idea can be combined with some knowledge of envelopes to produce a device that traces out an exact hexagon. The simulations are available at
http://demonstrations.wolfram.com/GenevaDriveMalteseCross,
http://demonstrations.wolfram.com/DrillingASquareHole,
http://demonstrations.wolfram.com/SquareHoleDrillInThreeDimensions, and
http://demonstrations.wolfram.com/DrillingAHexagonalHole.
Fibonacci's Forgotten Number Revisited
Richard Maruszewski
In 1225 Fibonacci visited the court of the Holy Roman Emperor, Frederick II. Because Frederick was an important patron of learning, this visit was important to Fibonacci. During the audience, Frederick's court mathematician posed three problems to test Fibonacci. The third was to find the real solution to the equation: x3 + 2x2 + 10x = 20 In an earlier article in this JOURNAL, Brown and Brunson discussed several methods that Fibonacci might have used to find his estimate for the solution to this problem and conjectured that the method of Elchataym was the one that Fibonacci actually used. This article continues this discussion and proposes another method, not mentioned by Brown and Brunson, but likely known to Fibonacci and more likely to be the one that he used.
Pompeiu's Theorem Revisited
Arpad Benyi, Ioan Casu
Pompeiu's theorem states that if ABC is an equilateral triangle and M a point in its plane, then MA, MB, and MC form a new triangle. In this article, we have a new look at this theorem in the realm of arbitrary triangles. We discover what we call Pompeiu's Area Formula, a neat equality relating areas of triangles determined by the points A, B, C, and M.
The Fresnel Integrals Revisited
Hongwei Chen
This note presents another elementary method to evaluate the Fresnel integrals. It is interesting to see that this technique is also strong enough to capture a number of pairs of parameter integrals. The main ingredients of the method are the consideration of some related derivatives and linear di?erential equations.
Maximizing the Spectacle of Water Fountains
Andrew J. Simoson
For a given initial speed of water from a spigot or jet, what angle of the jet will maximize the visual impact of the water spray in the fountain? This paper focuses on fountains whose spigots are arranged in circular fashion, and couches the measurement of the visual impact in terms of the surface area and the volume under the fountain's natural suggested surface (i.e., the surface of revolution of any one of the streams of water about the central axis of the fountain). Pappus' two theorems involving the centroid of an arc and of an area are used as keys to answer the question. The critical angle is, in general, other than 60 degrees.
Summations involving Binomial Coefficients
Hidefumi Katsuura
We prove following two conjectures of Thomas Dence:
Conjecture 1: Let n and k be odd positive integers with k ≤ n . Then

. Conjecture 2: Let n and k be even positive integers with k ≤ n . Then
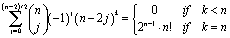
False Position, Double False Position and Cramer's Rule
Eugene Boman
We state and prove the methods of False Position (Regula Falsa) and Double False Position (Regula Duorum Falsorum). The history of both is traced from ancient Egypt and China through the work of Fibonacci, ending with a connection between Double False Position and Cramer's Rule.
CLASSROOM CAPSULES
Average Perceived Class Size and Population Density
Clifford H. Wagner
It is claimed that mean class size, as perceived by students, is always greater than a school's advertised average class size. This article gives a new, quick proof, and goes beyond previous inquiries to consider the perceptions of students taking multiple classes, It then develops a generalization for average population densities within a state or region. As a bonus, the discussion invokes famous inequalities by Chebyshev and Cauchy.
Differentiating the Arctangent Directly
Eric Key
We show by a direct argument that the inverse tangent function is differentiable at all values in its domain.
Finding Matrices Which Satisfy Functional Equations
Scott Duke Kominers
We discuss a method for constructing solutions of analytic functional equations in matrix functions. The approach combines elements of calculus and linear algebra: Taylor series and nilpotent matrices. As an example, we obtain a non-constant matrix function solving the functional equation N(2x)-(N(x))8=0.
PROBLEMS AND SOLUTIONS
BOOK REVIEWS
MEDIA HIGHLIGHTS




