- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The College Mathematics Journal - May 2012
In this issue of The College Mathematics Journal Michael Augros rediscovers Pascal’s mystic hexagon, Jacob A. Siehler provides a guided tour of the finite lamplighter groups, Carl Swenson and André L. Yandl partition Pythagorean triangles using Pythagorean angles, Donald Teets explains how push-to telescopes find astronomical objects, and David Benko reveals that the Basel problem is a telescoping series.
Rediscovering Pascal's Mystic Hexagon
Michael Augros
While the path to mathematical discovery is often intuitive and not simply reducible to the application of a method, neither is it in most cases entirely haphazard. Certain kinds of questions and certain ways of looking at things tend to produce new and interesting results. To illustrate, this paper tells a story of how someone might discover Pascal's Mystic Hexagon.
The Finite Lamplighter Groups: A Guided Tour
Jacob A. Siehler
In this article, we present a family of finite groups, which provide excellent examples of the basic concepts of group theory. To work out the center, conjuagacy classes, and commutators of these groups, all that's required is a bit of linear algebra.
Proof Without Words: The Square of a Balancing Number Is a Triangular Number
Michael A. Jones and Roger B. Nelsen
When Abelian = Hausdorff
Timothy Kohl
A pair of elementary exercises, one from topology, the other from group theory are such that if one replaces three words in the topology problem, you get the group theory problem and vice-versa. This suggests connections between the two that are explored here.
The Catenary as Roulette
Javier Sánchez-Reyes
The focus of a parabola rolling without sliding along a straight line traces a catenary. We give some historical notes on this classical kinematical construction, observe that it was rediscovered in a recent article, and give a simpler and more geometric alternative derivation.
Partitioning Pythagorean Triangles Using Pythagorean Angles
Carl E. Swenson and André L. Yandl
Inside any Pythagorean right triangle, it is possible to find a point M so that drawing segments from M to each vertex of the triangle yields angles whose sines and cosines are all rational. This article describes an algorithm that generates an infinite number of such points.
Proof Without Words: The Pythagorean Theorem with Equilateral Triangles
Claudi Alsina
Push-To Telescope Mathematics
Donald Teets
Two coordinate systems are related here, one defined by the earth's equator and north pole, the other by the orientation of a telescope at some location on the surface of the earth. Applying an interesting though somewhat obscure property of orthogonal matrices and using the cross-product simplifies this relationship, revealing that a surprisingly small amount of information is needed for the telescope controller to locate objects in the night sky.
The Distribution of the Sum of Signed Ranks
Brian Albright
We describe the calculation of the distribution of the sum of signed ranks and develop an exact recursive algorithm for the distribution as well as an approximation of the distribution using the normal. The results have applications to the non-parametric Wilcoxon signed-rank test.
Harmonic Series Meets Fibonacci Sequence
Hongwei Chen and Chris Kennedy
The terms of a conditionally convergent series may be rearranged to converge to any prescribed real value. What if the harmonic series is grouped into Fibonacci length blocks? Or the harmonic series is arranged in alternating Fibonacci length blocks? Or rearranged and alternated into separate blocks of even and odd terms of Fibonacci length?
The Basel Problem as a Telescoping Series
David Benko
The celebrated Basel Problem, that of finding the infinite sum 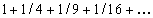 , was open for 91 years. In 1735 Euler showed that the sum is
, was open for 91 years. In 1735 Euler showed that the sum is 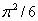 . Dozens of other solutions have been found. We give one that is short and elementary.
. Dozens of other solutions have been found. We give one that is short and elementary.
CLASSROOM CAPSULES
Designing Medical Tests: The Other Side of Bayes' Theorem
Andrew M. Ross
To compute the probability of having a disease, given a positive test result, is a standard probability problem. The sensitivity and specificity of the test must be given and the prevalence of the disease. We ask how a test-maker might determine the tradeoff between sensitivity and specificity. Adding hypothetical costs for detecting or failing to detect a disease, and employing software, we find the cutoff value for the test with the lowest social cost.
Quotient-Rule-Integration-by-Parts
Michael Deveau and Robie Hennigar
We present the quotient rule version of integration by parts and demonstrate its use.





