- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Benjamin Banneker's Trigonometry Puzzle - Conclusion
Because the logarithms in the worked examples are all to five decimal places, they do not seem to fit with any of the tables on page 3. However, it is instructive to examine the format of Briggs’s logarithms from Vlacq’s edition of 1628:
|
log 26 |
1, 41497, 33480 |
|
log(sin 30) |
9, 69897, 00043 |
|
log(sin 60) |
9, 93753, 06317 |
|
log(sin 90) |
10, 00000, 00000 |
Briggs himself defined the first (left-most) comma as standing in for the decimal point; subsequent commas, dividing the figures into groups of five, are merely placeholders to guide the eye. The logarithms in the worked example can be simply obtained merely by discarding the five right-most digits from the values given in the table. (As it happens, with the particular numbers chosen by Banneker, no rounding issue arises by the simple truncation of the tabular values.) It seems highly probable, therefore, that the logarithms used in the example did indeed come from the second edition of Briggs’s Arithmetica Logarithmica (Valcq, 1628), or its derivative, the Logarithmicall Arithmetike of 1634.
At the beginning of the seventeenth century, trigonometric functions were defined as follows:
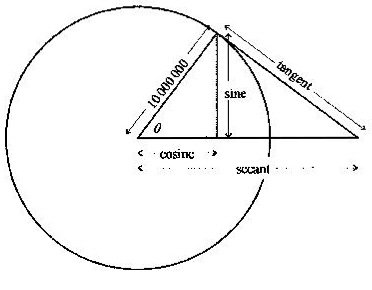
The radius of the circle was chosen so that the function values could be represented as integers to any desired degree of accuracy. Napier chose a radius of 107 (shown here); Briggs chose a radius of 1010. So, for Briggs, the sine of 90° (the whole sine or sinus totus) was 1010 and its (Briggsian) logarithm is, therefore, simply 10 ... and the logarithms of all the sines in the first quadrant are positive. In modern trigonometry, the radius is taken as unity – a convention unknown much before 1800 – so the sines of the angles in the interval [0°, 90°] are less than unity and their logarithms are, consequently, negative. The fact that the logarithms of sines in Briggs’s table are positive therefore arises naturally from the way in which the sine function was then defined.
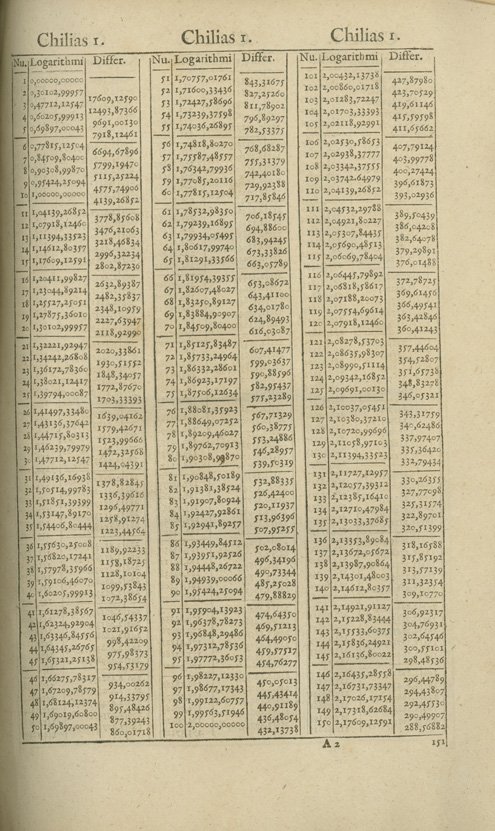
Image of a logarithm table from Briggs’s Arithmetica Logarithmica (Valcq, 1628), courtesy of Brenda Corbin, United States Naval Observatory, Washington, DC.
Florence Fasanelli, Graham Jagger, Bea Lumpkin, "Benjamin Banneker's Trigonometry Puzzle - Conclusion ," Convergence (June 2010)




