- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Parametric Plots: A Creative Outlet - Parameterizing Function Graphs
Parameterizing functions is easy. If y = f(x), then the parametric equations x(t) = t and
y(t) = f(t) always work. (That, is you simply treat x as the parameter). For example, if you want to parametrize the graph of the function f(x) = x3 + 2x2 - x + 9 from (0, 9) to (2, 23), then the parameterization is:
x(t) = t and y(t) = t3 + 2t2 - t + 9, 0
t
2.
Exercise 4.1

Figure 4.1 - The graph of a function
- Find a parameterization of the function shown in Figure 4.1. [Hint: The right-most point on the graph is (5
, 0).]
- Now find a parameterization that traces out the same curve in the reverse direction.
- Finally find a parameterization (x(t), y(t)) that satisfies x(0) = 0 and x(2) = 5
.
Exercise 4.2
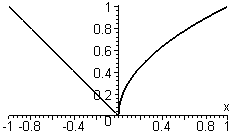
Figure 4.2 - A graph of a piecewise function
Find a parameterization of the piecewise-defined function shown in Figure 4.2. (Hint: This function can be plotted in two steps. Plot one piece on the MAPLET and then plot the other without clearing.)
Judy Holdener and Keith Howard, "Parametric Plots: A Creative Outlet - Parameterizing Function Graphs," Convergence (August 2004)




