- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Historical Activities for Calculus - Module 3: Optimization – Regiomontanus' Hanging Picture Problem
Regiomontanus' Hanging Picture Problem
Johann Müller (1436-1476), commonly known today as Regiomontanus, was perhaps the most influential mathematician of the fifteenth century. Although his contributions were mainly in the area of trigonometry, we are interested here in the following problem that he posed in a letter he wrote in 1471:
At what point on the ground does a perpendicularly suspended rod appear largest?
In other words, which point \(P\) on line \({\mathcal L}\) in Figure 40 below maximizes the angle \(APB?\)
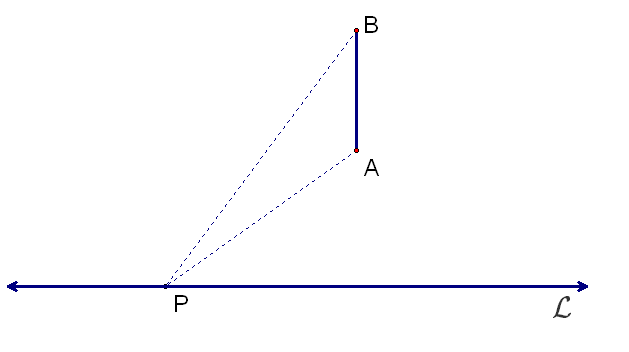
Figure 40. Regiomontanus' Problem: Which point \(P\) on \({\mathcal L}\) maximizes \(m\angle APB?\)
This problem was the first optimization problem that had appeared in the history of mathematics since the days of antiquity. It was probably inspired by questions of perspective that Renaissance artists of that time period were grappling with. It is often stated in modern calculus textbooks as follows:
A painting is hung flat against a wall. How far from the wall should one stand to maximize the viewing angle at his eye subtended by the painting?
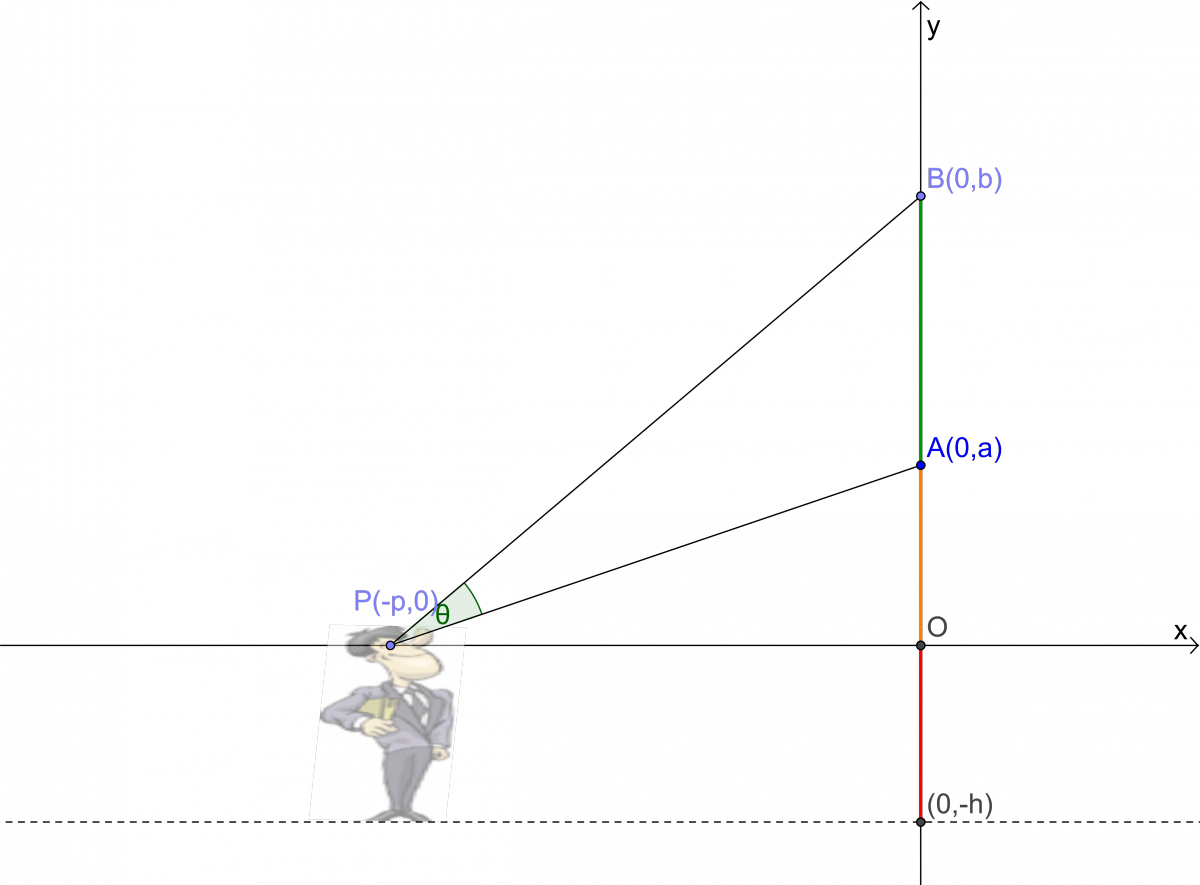
Figure 41. Modern equivalent of Regiomontanus' Problem: How far from a wall should an observer stand to maximize his viewing angle \(APB\) (or \(\theta\)) of a picture of height \(|AB|\) on the wall? Use the applet to identify the point \(P\) that maximizes \(m\angle APB\) for the example shown. Drag \(P\) horizontally to adjust the distance of the man from the wall. Next, note that you may adjust as well the height of the man, the height of the picture above the floor, and the height of the picture itself, respectively, by dragging points \(P,\) \(A,\) and \(B\) vertically.
Figure 42. To solve the Hanging Picture Problem more generally, we introduce a coordinate system and assign variables as shown.
In the picture in Figure 42, above, the line \({\mathcal L}\) (from Figure 40) is drawn at the height of the viewer's eye. We can impose a coordinate system on the scenario, with line \({\mathcal L}\) as the \(x\)-axis, and \(A\) and \(B\) (from Figure 40) on the \(y\)-axis, say \(A=(0,a)\) and \(B=(0,b).\) Then the height of the painting is \(b-a\) and the bottom edge of the painting is \(a+h\) units above the floor, where \(h\) is the height of the viewer's eye above the floor.
The original solution to this problem, like Heron's solution to the shortest distance problem, was geometric and did not use calculus. Consider a circle that goes through points \(A\) and \(B\) and is tangent to the line \({\mathcal L}\) (the \(x\)-axis). Let \(P\) be the point of tangency. Then \(P\) is the point on \({\mathcal L}\) that maximizes angle \(APB.\)
Figure 43. Geometric solution to Regiomontanus' Problem: \(P\) should be such that line \({\mathcal L}\) is tangent to the circle through \(P,\) \(A,\) and \(B.\)
To see this, let \(P^{\prime}\) be another point on \({\mathcal L}.\) We claim that \(m\angle 5>m\angle 3.\) Let \(H\) be the point of intersection of the circle and \( P^{\prime}B.\) Then \(m\angle 2=m\angle 5\) since both angles subtend the same chord. Also, \(m\angle 1 +m\angle 2=m\angle 1+m\angle 3+m\angle 4,\) since both equal \(180\) degrees. Subtracting \(m\angle 1\) from both sides gives \(m\angle 2=m\angle 3+m\angle 4.\) Hence
\[m\angle 5=m\angle 2=m\angle 3+m\angle 4>m\angle 3,\]
as was to be shown.
Exercises
Exercise 11.
Use calculus and a CAS to find the solution of Regiomontanus' Hanging Picture Problem. You need to find the value of \(x\) that maximizes \(\theta\) in the diagram below.
Figure 44. Regiomontanus' Hanging Picture Problem for Exercise 11
Here's one way to proceed: Since \(f(x)=\tan x\) is an increasing function, it is equivalent to maximize \[\tan\theta=\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}.\]
You should be able to rewrite this last expression all in terms of \(x,\) \(a,\) and \(b.\) Then use calculus to find the value of \(x\) that maximizes this quantity.
Exercise 12.
Suppose a six-foot tall adult comes to the museum with his three-foot tall child. They go into a room where a large 12-foot high painting is hung on the wall so that the bottom edge of the painting is 8 feet from the floor.
(a) How far from the painting should each of them stand in order to maximize their individual viewing angles?
(b) Compute each of their maximal viewing angles. Express your answer in degrees.
Figure 45. Applet for Exercise 12, part c. Drag \(I\) to adjust the height of the man. Drag \(A\) and \(B\) to adjust the height of the picture. Drag \(P\) to adjust the distance of the man from the wall.
(c) The applet in Figure 45 illustrates Regiomontanus' Hanging Picture Problem, with the line segment \(AB\) denoting the height of the picture, and the \(x\)-axis representing eye level. Check the box to show the circle through \(A\) and \(B\) tangent to the horizontal axis at eye level. Verify that the point of tangency is the solution to Regiomontanus' Problem by dragging the man's eye to that point and verifying that \(m\angle APB\) equals the maximal viewing angle you found above for the six-foot adult. Repeat for the three-foot child.
Gabriela R. Sanchis (Elizabethtown College), "Historical Activities for Calculus - Module 3: Optimization – Regiomontanus' Hanging Picture Problem," Convergence (July 2014)