- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
James Gregory and the Pappus-Guldin Theorem - A Ratio Between the Trunk and the Solid of Revolution
Gregory treats separately the ratio between the trunk and the solid of revolution and the ratio between the trunk and the cylinder. The key to understanding the first ratio is Cavalieri's Principle: "If two plane (or solid) figures have equal altitudes, and if sections made by lines (or planes) parallel to the bases and at equal distances from them are always in the same ratio, then the plane (or solid) figures also are in this ratio". (See [10, pp. 315-321], cited in [11, p. 516].) Once Gregory establishes a fixed ratio between corresponding slices of the trunk and the solid of revolution, this principle will imply that the solids themselves have the same ratio. He begins with the trunk, slicing it by an arbitrary plane OPV perpendicular to the axis of rotation.
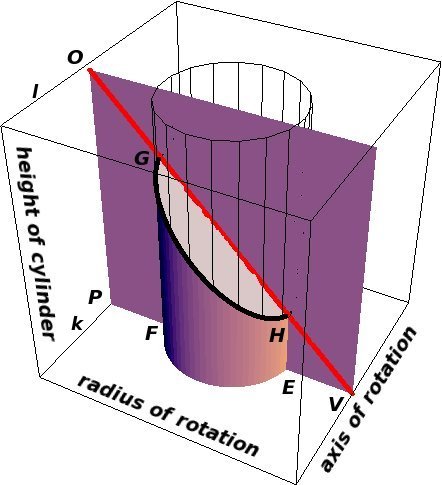
Let V denote the point of intersection of OPV with the axis of rotation and let O and P denote the intersections of OPV with l and k, respectively. Then
\[OP = \mbox{height of the cylinder} \]
and
\[PV = \mbox{radius of rotation}\]
Note that the values of OP and PV will not change no matter what the choice of the perpendicular plane OPV, but the intersection of OPV with the trunk will form a trapezoid EFGH which will vary in size as OPV moves along the axis of rotation. By similar triangles,
\[\frac{OP}{ PV} = \frac{GF}{FV} \]
and
\[\frac{OP}{ PV} = \frac{HE}{EV}\]
Multiply the first equality by \(\frac{1}{2\pi}\). Then some elementary arithmetic shows that
\[ \begin{eqnarray} \frac{OP}{2 \pi PV} = \frac{GF}{2 \pi FV} & \Rightarrow & \frac{OP}{2 \pi PV} = \frac{GF}{\pi FV} \cdot \frac{\frac{1}{2} FV}{ \frac{1}{2} FV } \cr\cr& \Rightarrow & \frac{OP}{2 \pi PV} = \frac{\frac{1}{2} GF\cdot \ FV}{\pi FV^2} \cr\cr & \Rightarrow & \frac{OP}{ 2 \pi PV} = \frac{area(\Delta GFV) }{area(circle(FV))}\end{eqnarray},\]
where \(\Delta\)GFV denotes the triangle GFV and circle(FV) denotes the circle on radius FV.
The second equality shows similarly that
\[\frac{OP}{2 \pi PV} = \frac{area(\Delta HEV)}{area(circle(EV))}\]
Consequently, by applying Euclid V.19 to these two ratios,
\[\frac{OP}{2 \pi PV} = \frac{area(GHEF)}{area(annulus(FV - EV))}\]
where area(GHEF) denotes the area of the trapezoid GHEF and area(annulus(FV - EV)) denotes the area of the annulus obtained by revolving the segment EF around the axis of rotation. Note that the numerator on the right is a slice of the trunk and the denominator is the corresponding slice of the solid of revolution. Since OP and PV do not change, it follows by Cavalieri's principle that the ratio of the volume of the trunk to the volume of the solid of revolution is equal to the ratio of OP to 2\(\pi\)PV.
To be more specific, if AB is any planar figure let rev(AB) denote the volume of the solid of revolution obtained by revolving AB around an axis of revolution and trunk(AB) denote the volume of a trunk of a right cylinder over AB. Then
\[\frac{trunk(AB)}{ rev(AB)} = \frac{OP}{2 \pi PV}\]
If OP = height(AB) is the height of the cylinder over AB and \(2 \pi \)PV = circum(AB) is the circumference of the circle with radius equal to the radius of rotation for AB, then we can write
\[\frac{ trunk(AB)}{rev(AB)} = \frac{ height(AB)}{ circum(AB)}\]
This is the sought after ratio between the solid of revolution and a trunk constructed from the same 2-dimensional figure.
This formula also yields a way to describe the ratio between the volumes of two solids of revolution--something quite important for someone brought up to appreciate Euclidean proportion theory. Suppose, for instance, that AB and EF are two planar figures extended into 3-dimensions to form cylindrical figures which by assumption have the same height.
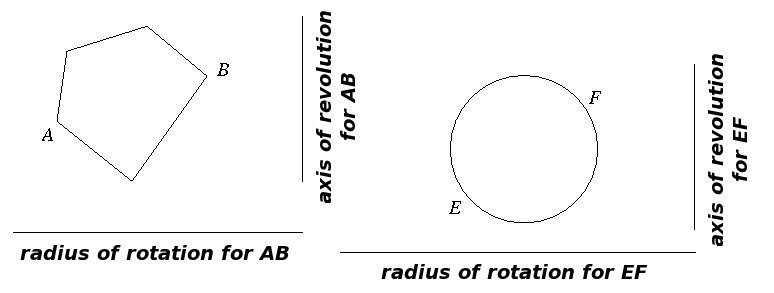
Using the notation from above, the previous result implies that
\[\frac{trunk(AB)}{rev(AB)} = \frac{height(AB)}{circum(AB)}\]
and
\[\frac{trunk(EF)}{rev(EF)} = \frac{height(EF)}{circum(EF)}\]
Since height(AB) = height(EF) by assumption, we eliminate the common value from both equations to arrive at
\[\frac{rev(AB)}{rev(EF) } = \frac{trunk(AB)}{trunk(EF)} \cdot \frac{circum(AB)}{circum(EF)},\]
This shows that the ratio between solids of revolution can be understood completely in terms of trunks and radii of rotation.
Andrew Leahy (Knox College), "James Gregory and the Pappus-Guldin Theorem - A Ratio Between the Trunk and the Solid of Revolution," Convergence (February 2010), DOI:10.4169/loci003262




