- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Ancient Chinese Contribution
Ancient Chinese mathematics was often used to meet the imperial needs of engineering, land mensuration, calendar reckoning, military campaigns, and water control and conservancy [5, 7]. The oldest extant Chinese mathematical treatise, the Zhou bi suan jing (Mathematical Classic of the Zhou Gnomon), written around 100 BCE - 100 CE , is devoted primarily to astronomical and calendrical matters. The title of this work has also been translated as The Arithmetical Classic of the Gnomon and Circular Paths of Heaven, while astronomers themselves in China were dubbed "surveyors of the heavens." The text contains results on right triangles, such as gou-gu relations, and discusses the use of measuring instruments, such as the L-shaped set-square or gnomon. This device along with appropriate measurements and proportionality results for similar triangles allowed the determination of distances to inaccessible points [7].
The practice of mathematics in ancient China acquired a mythical, if not a purely utilitarian status. The legendary emperor-engineer Yu the Great, depicted holding a set-square, is claimed to have accomplished much via the use of mathematics:
Emperor Yu quells the floods, he deepens the rivers and streams, observes the shape of mountains and valleys, surveys the high and low places, relieves the greatest of calamities and saves the people from danger. He leads the floods east into the sea and insures no flooding or drowning. This is made possible because of the gou-gu theorem [8, p. 29-30].
A second classic, the Jiu zhang suan shu (The Nine Chapters on the Mathematical Art), is a compilation of mathematical techniques known or developed between the eleventh century BCE and 220 CE. More of a reference manual or study guide, the text contain 246 problems ranging from computing with fractions to finding the area of rectangular fields to applications of the gou-gu relation. The third century scholar, Liu Hui, sometimes referred to as "the Chinese Euclid," compiled an edition of the Jiu zhang suan shu that became rather influential in China, and was used at the Imperial College during the Tang dynasty (618-907) [5, p. 227].
Additionally and significantly, Liu authored the Hai dao suan jing (The Sea Island Mathematical Manual) [7], which was written as an addendum to the Jiu zhang suan shu, but eventually appeared separately. Recognized as an original contribution to the art of surveying, the Hai dao suan jing develops a method of determining the height of an unknown object based on sightings from two poles of equal (known) height, a fixed distance apart, that was applied to computing such fanciful calculations as the height of the sun. The method, called chong cha or "double difference" can be used to find the height PQ given the lengths AS = CN (the "poles"), SB, ND (the "shadows"), and SN below (Figure 3). The result PQ is expressed in terms of the height AS and the two differences ND - SB and QN - QS = SN, so that the actual distances of S and N from the point Q need not be known, as long as the distance between the poles, SN, is known. The verification requires two applications of proportionality results for similar triangles (see Extra Credit A of Section 4.)
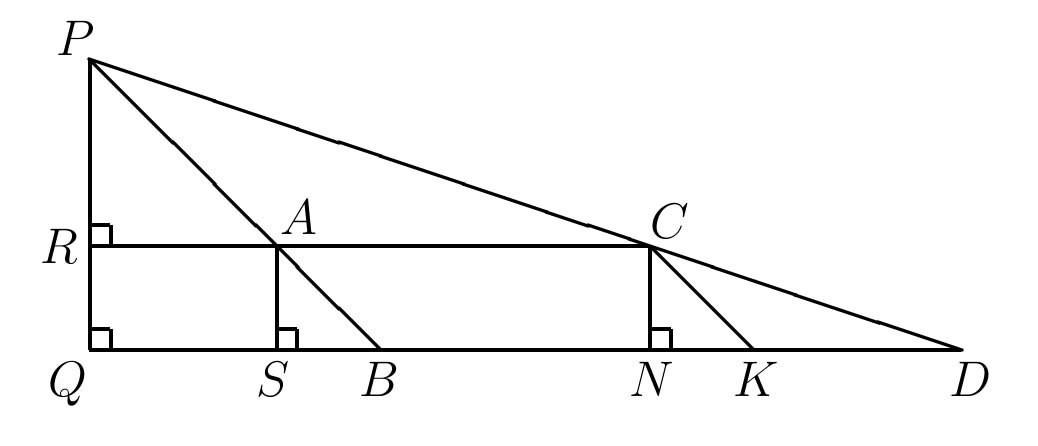
Figure 3: The Chong Cha Method
Let's examine an area argument appearing in the Zhou bi suan jing and the Jiu Zhang suan shu referred to as the "in-out" principle [5] or the "inclusion-exclusion" principle. This may be interpreted as a duality statement, where one part of a figure corresponds to an often congruent dual or counterpart in the same figure. Consider rectangle ABCD with diagonal BD (Figure 4).
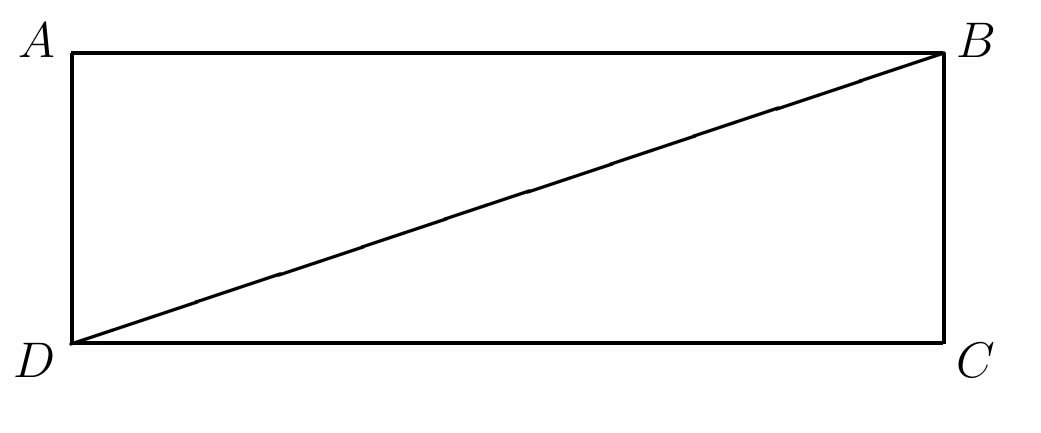
Figure 4: Rectangle ABCD.
Then triangles ABD and CDB have the same area, since they are congruent. On the diagonal BD choose a point H, and draw JK through H parallel to AB, and draw LM through H parallel to BC. The inclusion-exclusion principle states that figures \(III\) and \(III^{\prime},\) i.e. rectangles ALHJ and HKCM, have the same area (Figure 5).
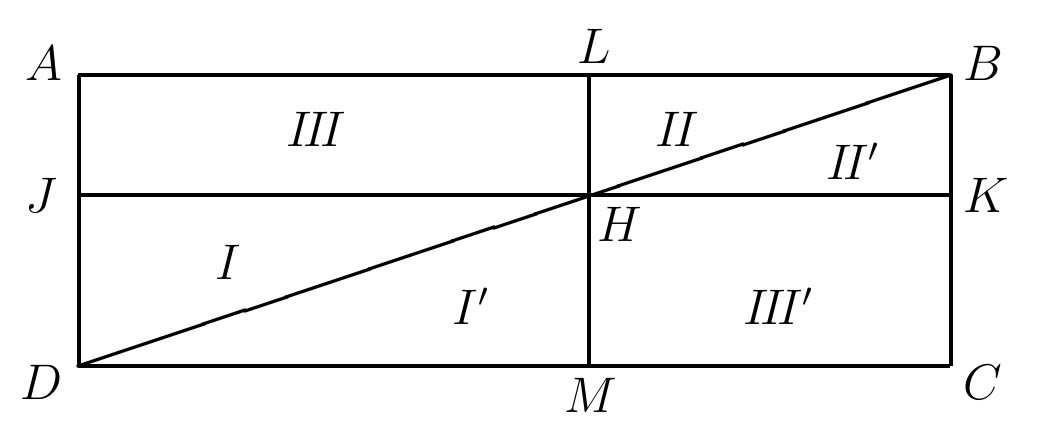
Figure 5: The "In-Out" Principle.
This follows since triangles \(I\) and \(I^{\prime}\) are congruent, and thus have the same area, while triangles \(II\) and \(II^{\prime}\) also have the same area. Deleting \(I\) and \(II\) from triangle ABD, and deleting \(I^{\prime}\) and \(II^{\prime}\) from triangle CDB, it follows that \(III\) and \(III^{\prime}\) have the same area.
Jerry Lodder (New Mexico State University), "Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Ancient Chinese Contribution," Convergence (July 2010)




