- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Servois' 1813 Perpetual Calendar, with an English Translation - Translation of Servois' 'Perpetual Calendar'
Perpetual Calendar1
By Mr. Servois, professor of the artillery schools*
[84]2 The calendar, whose uses I shall explain, may be used to solve this general question, which includes four particulars: Of [85] these four things: if any of these three are given: a year of the common era, the name of a month of that year, a day of the month, and the name of the day of the week which corresponds to this day, then what is the fourth?
I shall provide some examples, which are always much more clear than explanations, and will demonstrate the advantages that can be drawn from this little calendar (See the plate [Figure 9]).
PROBLEM I. Determine which day of the week corresponds to a certain day of a designated month of a given year?
Example. We wish to know, which day of the week corresponds to January 28, 1821?
In the table, look for the column that includes the number 21 with which the year terminates; you will find that this is the first on the left. In the same column look for the word January, which you will find at the top, followed by October. Then, move horizontally along the first line until you find yourself vertically above the last of the medallions at the bottom, which contains only the date given 28. You will find the word Sunday on the circle at which you will stop, and will tell you that January 28, 1821 will be a Sunday.

Figure 9. Servois' perpetual calendar appeared on page 92 of the Annales.
Remark. If the year is a leap year, that is to say, if the number formed by its last two digits on the right is a multiple of 4, then during the first two months, January and February, we must make use of the column that immediately precedes, on the left, the column that contains the indication, and use the last one if this column is the first one. This is a general remark.
Thus, for example, if we wanted to find the day of the week that corresponds to January 28, 1824, then because 24, which belongs in the 5th column, is a multiple of 4, and because January is one of the first two months, we must make use of the 4th column. There we find January followed by October in the fourth circle down. Then moving horizontally to the right until the last [86] column, below which the day 28 is found, the word Wednesday that we find in the circle upon which we stopped, tells us that January 28, 1824 must be a Wednesday.
PROBLEM II. To determine which days of a designated month, in a given year, correspond to a certain day of the week?
Example. We wish to know, what are the days in February which will be Sundays in the year 1836?
Because 36 is in the 6th column and is a multiple of 4, and because February is one of the first two months, I am using the 5th column. I look there for the word February that is at the top, followed by March and November, and I move horizontally until the word Sunday, which belongs to the last column. Otherwise, I look for the word Sunday in the 5th column, and I again move horizontally until I meet the word February. I fall once again on the last column and I read at the bottom that the Sundays in February 1836 will be 7, 14, and 21.
PROBLEM III. To determine which are the months of a designated year, in which a certain day of the week corresponds to a certain date?
Example. We wish to know, what are the months of the year 1825 that will begin on a Monday?
25 is found to belong to the 6th column in which I look for the word Monday. I move horizontally to the left, starting from this word, until I meet the first column, under which I find the day numbered 1, and I read in this circle that there is but the single month of August in the year 1825 that should begin on Monday.
If it were a matter of the year 1828, which is a leap your, we will first find the word Monday in the 2nd column, which immediately precedes the one that includes the number 28. Then moving to the left horizontally until the first column, below which lies the day numbered 1, we first find the months of April and July, which we reject, because they fall beyond the first two, and we had used the column that precedes the year. Then taking [87] the word Monday in the third column and moving horizontally to the first one, we meet the months of September and December, both of which we admit, because they fall after the first two, which are consequently the only ones of the year 1828 which begin on a Monday.
PROBLEM IV. To determine which are the years in which a certain day of the week coincides with a given date of a designated month?
Example. We wish to know in which years April 1st will be a Sunday?
The number 1 is found at the bottom of the first column and April is found in the lowest circle in this column, which also contains the word Sunday. We then conclude that the years that have April 1st on a Sunday are: 1804, 1810, 1821, 1827, 1832, 1838, 1849, 1855, 1860, 1866, 1877, 1883, 1888, 1894, etc.
Suppose it were a matter of one of the first two months of the year -- for example, if we wished to know which were the years in which the 7th of February is a Saturday. The number 7 is found in the last column, where the month February is in the 3rd circle. Then moving horizontally to the left, until the one that contains the word Saturday, we find that it is in the fourth column. However, we must reject all the leap years in this column and substitute the asterisks that we find there with the leap years of the next column, which gives 1801, 1807, 1818, 1824, 1829, 1835, 1846, 1852, 1857, 1863, 1874, 1880, 1885, 1891, etc.
Remark. This calendar is only prepared for the current century, but we will make it truly perpetual by a simple transposition of the numbers that express the years, from one column to another, in such a way that the number 00 is found in the 7th column, in the 5th, in the 3rd, or in the first column depending on whether the number to the left of the last two digits gives a remainder of 0, 1, 2, or 3 when divided by four, so that with only four tables, [88] we have a calendar that can be used for all centuries, past and future, at least until the error, presently negligible, does not become, by the accumulation of the centuries, large enough to require a new reform.**
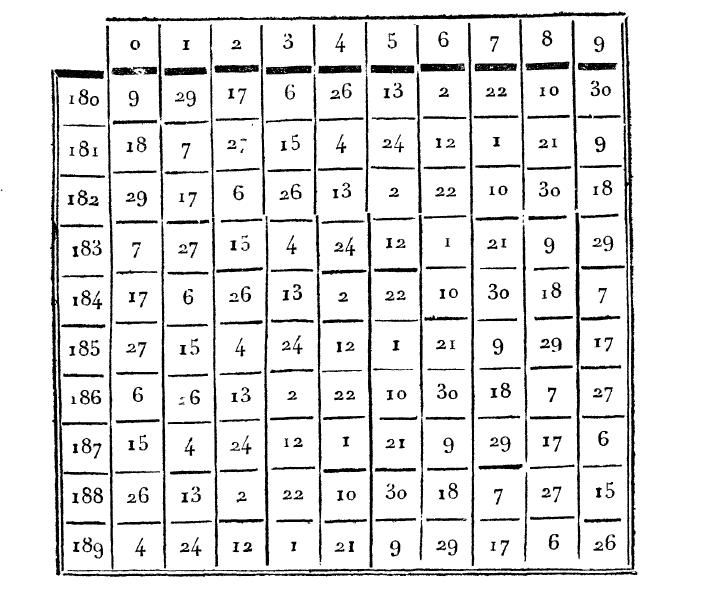
Mr. Gauss3 has given in the 2nd volume for 1802 of the excellent journal Astronomico-Géographique4 by the Baron de Zach,5 a method for calculating the epoch of Easter for each year. From this I deduced the following table,6 which would be easy to extend and which, for every year of the nineteenth century, gives the epoch of the full moon of March.
[89] The decades are to the left of the table and the units are above, as in tables of logarithms. Dates less than 20 belong to the month of April and the others to the month of March. The law of this table is very simple: by writing every one of the 30 days from March 21st to April 19th inclusive in a circle, these dates taken nineteen at a time, in the direct order, form the horizontal rows, and taken alternately nine at a time and ten at a time give the vertical columns.
Using this table, if we want to know the epoch of the full moon of March for the year 1854, we will find on the spot that it is April 12th. On the other hand, if we want to know in what years the full moon will fall on April 4th, we will find that this will occur in the years 1814, 1833, 1852, 1871, and 1890.
Also, as Easter is set as the Sunday that immediately follows the full moon of March, it is easy, using the combination of this little table with our calendar, to determine the epoch of Easter for each year and reciprocally to assign the years in which this feast falls on a designated epoch.
For example, if we want to know the epoch of Easter for the year 1852, because we have found that for this year, the full moon of March comes on April 4th and, as we have found elsewhere from the calendar, that April 4th is a Sunday, we then conclude that in 1852 Easter falls on April 11th.
[90] Conversely, if we ask in which years Easter will fall on April 1st, we have already seen that this day was a Sunday only in 1804, 1810, 1821, 1827, 1832, 1838, 1849, 1855, 1860, 1866, 1877, 1883, 1888, etc. On the other hand, in order that Easter falls on April 1st, the full moon of March must occur from March 26th to April 1st, inclusive, which occurs only in the years 1801, 1804, 1809, 1812, 1817, 1820, 1823, 1828, 1831, 1836, 1839, 1842, 1847, 1850, 1855, 1858, 1861, 1866, 1869, 1874, 1877, 1880, 1885, 1888, 1893, 1896, 1899, etc. Therefore, Easter will occur on April 1st only in the years 1804, 1855, 1866, 1877, 1888, etc.
* It was only through the plea of the editor of the Annales that Mr. Servois who had sent him this ingenious calendar, without attaching the least importance to it, was willing to permit it to appear in this journal, in which we think that it would not at all be out of place.
** I do not know if it has yet been remarked that the Persian intercalation, I mean that of 8 days over 33 years, slightly more accurate than the Gregorian intercalation, could be brought back in a completely remarkable way because of its precision and uniformity. To do this would require adding one day every four years, to delete it every century, to restore it every four centuries, to delete it every ten thousand years, to restore it every forty thousand years, and so on. Indeed, this would give the length of the mean year as, \[365^j + \frac{1}{4} - \frac{1}{100} + \frac{1}{400} - \frac{1}{10000} + \frac{1}{40000} - \ldots\] or \[365^j + \left(\frac{1}{4} + \frac{1}{400} + \frac{1}{4000} + \ldots \right) - \left(\frac{1}{100} +\frac{1}{10000} + \ldots \right)\] or \[365^j + \frac{25}{99} - \frac{1}{99} = 365^j + \frac{24}{99} = 365^j + \frac{8}{33}.\] J.D.G.7
- Calendrier perpétuel, an article in Annales des Mathématiques pures et appliquées 4 (1813-1814), pp. 84-90. Some citations might begin with the word Chronologie because the headline in Gergonne's Annales is the editorial category to which the article was assigned.
- Numbers in square brackets represent the original page numbers of the article in Gergonne's Annales.
- Johann Carl Friedrich Gauss (1777-1855).
- Servois stated that Gauss' article [1800] appeared in the Astronomico-Géographique; however, this paper actually appeared in the Monatliche Correspondenz. Around 1813, the Monatliche Correspondenz was no longer going to put out publications and there were discussions of renaming the journal to Astronomico-Géographique; however, this never occurred. Interestingly, Zach started a new journal in 1818 named Astronomico-Géographique. Also, there appears to be a typographical error on Servois' part. Servois claimed that the paper appeared in the 2nd volume of the journal in 1802; however, this paper appeared in 1800.
- Baron Franz Xaver von Zach (1754-1832).
- Image used courtesy of the Science, Industry and Business Library of the New York Public Library.
- In this footnote, Gergonne used the superscript \(j\) to symbolize the word jours, which means days.
Salvatore J. Petrilli, Jr. (Adelphi University), "Servois' 1813 Perpetual Calendar, with an English Translation - Translation of Servois' 'Perpetual Calendar'," Convergence (June 2012), DOI:10.4169/loci003884