- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Polygons in Euclid's Elements, Book I
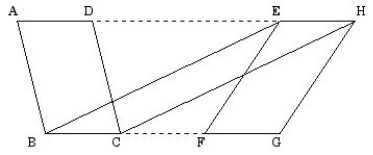
Proposition I.36.1] Parallelograms which are on equal bases and in the same parallels equal one another.2
Let ABCD and EFGH be parallelograms which are on the equal bases BC and FG and in the same parallels AH and BG.
I say that the parallelogram ABCD equals EFGH.3
Join BE and CH.4
Since BC equals FG and FG equals EH, therefore BC equals EH.
But they are also parallel, and EB and HC join them. But straight lines joining equal and parallel straight lines in the same directions are equal and parallel, therefore EBCH is a parallelogram.5
And it equals ABCD, for it has the same base BC with it and is in the same parallels BC and AH with it.6
For the same reason also EFGH equals the same EBCH, so that the parallelogram ABCD also equals EFGH.
Therefore parallelograms which are on equal bases and in the same parallels equal one another. QED7
[Proposition I.38.] Triangles which are on equal bases and in the same parallels equal one another.
Let ABC and DEF be triangles on equal bases BC and EF and in the same parallels BF and AD.
I say that the triangle ABC equals the triangle DEF.
Produce AD in both directions to G and H. Draw BG through B parallel to CA, and draw FH through F parallel to DE.
Then each of the figures GBCA and DEFH is a parallelogram, and GBCA equals DEFH, for they are on equal bases BC and EF and in the same parallels BF and GH.
Moreover the triangle ABC is half of the parallelogram GBCA, for the diameter AB bisects it. And the triangle FED is half of the parallelogram DEFH, for the diameter DF bisects it.
Therefore the triangle ABC equals the triangle DEF.
Therefore triangles which are on equal bases and in the same parallels equal one another. qed
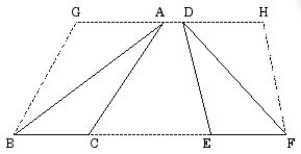
[Proposition I.42] To construct a parallelogram equal to a given triangle in a given rectilinear angle.8
Let ABC be the given triangle, and D the given rectilinear angle.
It is required to construct in the rectilineal angle D a parallelogram equal to the triangle ABC.
Bisect BC at E, and join AE. Construct the angle CEF on the straight line EC at the point E on it equal to the angle D.9 Draw AG through A parallel to EC, and draw CG through C parallel to EF.
Then FECG is a parallelogram.
Since BE equals EC, therefore the triangle ABE also equals the triangle AEC, for they are on equal bases BE and EC and in the same parallels BC and AG.10 Therefore the triangle ABC is double the triangle AEC.
But the parallelogram FECG is also double the triangle AEC, for it has the same base with it and is in the same parallels with it,11 therefore the parallelogram FECG equals the triangle ABC.
And it has the angle CEF equal to the given angle D.
Therefore the parallelogram FECG has been constructed equal to the given triangle ABC, in the angle CEF which equals D. QEF12
Footnotes:
1 The text is Sir Thomas Heath's well-known English translation. We adopt the common convention of referring to propositions from the Elements by book and number, whence I.36 refers to the 36th proposition of Book I.
2Notice that it is the areas of the parallelograms that are being discussed here; Euclid makes no distinction between the area of the figure and the figure itself. Further, the statement of the proposition makes it clear that the area of a parallelogram depends only on the length of its base and its corresponding height (the distance between the parallels to which reference is made in the statement of the proposition). This is clear to the modern geometer when she writes that the formula for the area of a parallelogram with base b and height h is A = bh. But Euclid is not a modern geometer, so he sees no need to make reference to the (numerical) height of the parallelogram when the purely geometric form of the pair of parallels enclosing the figure is description enough for him. Euclid does not compute the area of the figure, he simply characterizes it in terms of its "elements."
3It will be obvious from the style of the writing, here and throughout the Elements, that Euclid adopts a very formal style of writing, almost like poetic verse, to lay out geometric propositions. The initial statement of the proposition, given in italics in the text, is called the protasis. It identifies the premises or conditions and the corresponding conclusion of the proposition at hand, often (though not in this instance) in the form "If ... , then ... " The protasis is followed by a second version of the hypotheses of the proposition, the ekthesis, this time with letters referring to a specific, but entirely generic, illustration of the given data. The ekthesis is also accompanied by a diagram to which the letters refer. This is immediately followed by the diorismos, or restatement of the conclusion, often using the words "I say that ... " The remaining parts of the format for Euclidean propositions will be discussed in the next note.
4The fourth part of the propostion is called the kataskeu¯e (it need not appear in all propositions). It calls for any additional lines or curves that should be added to the diagram to help effect the proof. It is followed by the apodeixis, the meat of the proof, which lists the chain of reasons leading from the given premises to the final conclusion.
5Euclid calls here on the fact, which he has proved earlier (in Proposition I.33) that in a quadrilateral, if one pair of opposite sides is parallel and equal, then so must the other pair be.
6Euclid also cites an earlier proposition here to justify this step of the argument. But it is easy enough to see the reason directly from the diagram: since triangles ABE and BCH have equal dimensions (see the figure), then they are clearly equal, and removing each of these triangles in turn from the trapezoid ABCH leaves the parallelograms ABCD and EBCH, which must therefore also be equal.
7The final sentence of the proposition is called the sumperasma; it is simply a recapitulation of the original statement of the proposition, prefaced with a "therefore," and typically followed by the phrase "which was to be demonstrated" (in Latin, quod erat demonstrandum, often abbreviated as QED).
8The form of the statement of this proposition is different from that of the two previous propositions we have displayed here. Whereas Propositions I.36 and I.38 are what are technically called theorems, or assertions of mathematical fact, Proposition I.42 is what the Greeks called a problem, in which the goal is to find some desired point, line, figure, or number. All of Euclid's propositions have one of these two forms.
9Euclid, in I.23, showed how to construct a copy of a given angle along a given line at any particular point on it. It is a straightforward construction procedure.
10You recognize this as precisely the content of Proposition I.38.
11Euclid has established this - that the triangle whose base is the same as a given parallelogram and whose opposite vertex lies on the extensions of the opposite and parallel side of the parallelogram is equal to half the parallelogram - in Proposition I.41. In other words, if a triangle has base b and height h, and a parallelogram has the same dimensions, then the area of the triangle (A = [1/2]bh) is exactly half that of the parallelogram (A = bh).
12Since this proposition is a problem, not a theorem, the sumperasma ends with the phrase "which was to be constructed," in Latin, "quod erat factum."
Daniel E. Otero (Xavier University), "The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Polygons in Euclid's [i]Elements,[/i] Book I," Convergence (July 2010)