- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Thomas Simpson and Maxima and Minima - Motion of bodies II
Let a body move uniformly from A towards Q, with the celerity m, and let another body proceed from B, at the same time, with the celerity n. Now it is proposed to find the direction BP of the latter, so that the distance MN of the two bodies, when the latter arrives in the way of direction AQ of the former, may be the greatest possible (Example XIV, page 31).
Draw the perpendicular \(\overline{BC}\) and let \(b = BC, a = AC\). Let \(N\) be the point where the second body crosses the path from \(A\) to \(Q\), and define \(x = BN, \alpha = m \angle CBN\). Let \(M\) be the position of the first body when the other is at \(N\).
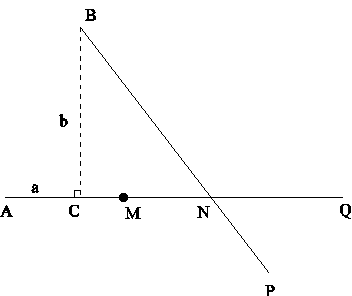
Since \(M\) and \(N\) are cotemporary we will have \(\frac{AM}{m} = \frac{BN}{n}\). Thus \(AM = \frac{m}{n}x\), and consequently \(CM = AM - AC = \frac{m}{n}x - a\). Then \(MN(x) = CN - CM = \sqrt{x^2 - b^2} - \frac{m}{n}x + a\). Taking the derivative and making it equal to zero we get
\(0 = MN'(x) = \frac{x}{\sqrt{x^2 - b^2}} - \frac{m}{n}\)
so \(MN\) adopts its maximum at \(x = \frac{mb}{\sqrt{m^2 - n^2}}\). Therefore
\(\cos \alpha = \frac{b}{x} = \frac{b}{\frac{mb}{\sqrt{m^2 - n^2}}} = \frac{\sqrt{m^2 - n^2}}{m}\).
Consequently \(\alpha = \arccos(\frac{\sqrt{m^2 - n^2}}{m})\) is the direction to be adopted by the second body if the distance \(MN\) is to be maximized.
Remarks: It is to be noted that
\(MN(\frac{mb}{\sqrt{m^2 - n^2}}) = \frac{na - b \sqrt{m^2 - n^2}}{n})\),
so we must have \(na - b \sqrt{m^2 - n^2} > 0\) in order to have a solution. Furthermore, one can check that
\(MN''(x) = \frac{-b^2}{(x^2 - b^2)^\frac{3}{2}}\);
therefore
\(MN''(\frac{mb}{\sqrt{m^2 - n^2}}) < 0\),
so indeed we are dealing with a maximum! Simpson assumes that \(m > n\). What happens if \(n \ge m\)? Under these circumstances there is not a mathematical solution. From a practical point of view, the body that starts at \(B\) would have to follow an angle \(\alpha = 90 - \varepsilon\) where \(\varepsilon\) is a very small positive number. On the other hand, Simpson only discusses the case when \(M\) is between \(C\) and \(N\). It can happen that \(M\) is between \(A\) and \(C\), in which case
\(MN = AN - AM = a + \sqrt{x^2 - b^2} - \frac{m}{n}x\)
(the very same expression for \(MN\) found before). If \(M\) is to the right of \(N\), then
\(MN = AM - AN = \frac{m}{n}x - (a + \sqrt{x^2 - b^2})\).
We note that
\(MN'(x) = \frac{m}{n} - \frac{x}{\sqrt{x^2 - b^2}}\).
Thus
\(0 = \frac{m}{n} - \frac{x}{\sqrt{x^2 - b^2}}\)
leads, as expected, to \(x = \frac{mb}{\sqrt{m^2 - n^2}}\).
A numerical example can further clarify the solution to the problem. Suppose \(m = 5\) mph, \(n = 4\) mph, \(b = 1\) mile, \(a = 20\) miles. Let \(t\) be the time it takes body \(B\) to reach the ray \(\overrightarrow{AQ}\) at a certain point \(N\). After \(t\) hours body \(A\) will be at \(M\), so \(\frac{AM}{5} = \frac{BN}{4}\). Therefore \(AM = \frac{5}{4}x\), where \(x = BN\). But \(AM + MN = AC + CN = 20 + \sqrt{x^2 - 1}\) . Hence \(\frac{5}{4}x + MN = 20 + \sqrt{x^2 - 1}\), i.e. \(MN(x) = 20 + \sqrt{x^2 - 1} - \frac{5}{4}x\). Taking the derivative and making it equal to zero we get \(\frac{x^2}{(x^2 - 1} = \frac{25}{16}\), thus \(x = \frac{5}{3}\). Finally, since \(\cos \alpha = \frac{1}{\frac{5}{3}} = \frac{3}{5}\), we get \(\alpha = \arccos(\frac{3}{5}) = 53.13\)°.

Editor’s Note: This article was published in 2005.
Michel Helfgott, "Thomas Simpson and Maxima and Minima - Motion of bodies II," Convergence (August 2010)




