- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
When a Number System Loses Uniqueness: The Case of the Maya - The Mayan Number System
The Mayan culture used a base \(20\) number system. It was an additive positional system that used two symbols, a dot for one, a horizontal bar for five, and a cowry shell for a place holder (it is unclear whether they also considered it a true numeric "zero''). Numbers were written vertically with the most significant digit at the top. They used a purely base \(20\) system for simple recording of commodities. However, their much more prevalent and culturally important calendar system used a modified base \(20\) system. The place values employed in this number system are tied to the Calendar Round and Long Count calendars. Each place represents the next order of numbers of days. So the first place, \(20^0,\) is days. The next, \(20^1,\) is months. The third would be years made up of \(20^2=400\) days. However, \(18\times20\) more accurately represents the year of 360 days (plus 5 Wayeb days) than does \(400,\) so here they used \(18\times20=360\) rather than \(20^2=400.\) Thus the Maya developed a modified base \(20\) system in which a date is represented by a number written (in modern Indo-Arabic notation) as: \[a.b.c.d.e=a(18\times20^3)+b(18\times20^2)+c(18\times20^1)+d(20^1)+e(20^0),\] where the third place value is not \(20^2\) but \(18\times20.\) After the third place, each higher place is \(20\) times the previous place value. So the system breaks only in the third place.
Since the Mayan system is base \(20,\) as in hex (base \(16\)), we need more than our ten digits to write their numbers. Standard modern practice for writing Mayan numbers is to write left to right with the most significant digit on the left, as in modern numeration, separating each place by a period. As an example using Indo-Arabic numerals for simplicity, we return to Isabel's birth date of \(5042006,\) which converts via the division algorithm to the Mayan numeral \(1.15.0.10.6\). This would be expanded as: \[1 (18 \times 20^3) + 15 (18 \times 20^2) + 0 (18 \times 20^1) + 10 (20^1) + 6 (20^0).\] This expansion shows clearly the modified nature of the Mayan calendric number system. Each place is a higher power of \(20\) except in the third place (what we would think of as the hundreds place in base \(10\) and should be \(20^2\) in base \(20\)) where a \(20\) has been replaced by an \(18.\)
Please note that the calculation above is simply the modern Gregorian date for Isabel's birthday converted into Mayan numerals; it is not the date in the Mayan Long Count. Since the focus of this article is the uniqueness of the Mayan number system, and not their dating system, we preferred to focus on the conversion of a number and not how to convert dates. However, there are various websites that will convert a modern date into a Mayan Long Count date. Using the Maya Astronomy Page [7], the Mayan date of Isabel's birthday is \(12.19.13.3.8,\) or \[12 (18 \times 20^3) + 19 (18 \times 20^2) + 13 (18 \times 20^1) + 3 (20^1) + 8 (20^0) = 1,869,548\] days into the \(1,872,000\)-day Long Count cycle.
In general, a natural number \(n\) would be expanded in the Mayan modified base \(20\) system as: \[a_0 + a_1 (20) + a_2 (18 \times 20) + a_3 (18 \times 20^2) + a_4 (18 \times 20^3) + \cdots + a_k (18 \times 20^{k-1}),\] but would be encoded \(a_k. \cdots .a_3.a_2.a_1.a_0,\) again with the most significant digit on the left.
Below is an example of a Serpent Date found in the Dresden Codex.
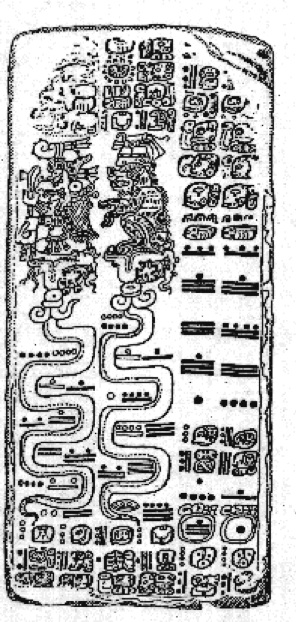
Figure 2. Page from the Dresden Codex showing two Serpent numbers [5]
Two serpents are shown, each depicting two numbers or dates (one in black and one in outline). To read these "bar and dot" Maya numerals, we need to know only that bars represent \(5\)'s and dots \(1\)'s (and cowry shells \(0\)). Thus the numeral just to the right of the tail of the righthand serpent consisting of three bars and four dots is \(3\times5+4\times1=19,\) the largest Maya "digit". Taking the black number in the right serpent we have: \[4 (18 \times 20^4) + 6 (18 \times 20^3) + 9 (18 \times 20^2) + 15 (18 \times 20^1) + 10 (20^1) + 19 (20^0)\] \[= 12,449,559\] in base \(10.\) Figure 3 shows the Serpent number for Isabel's birth date, \(1.15.0.10.6\).
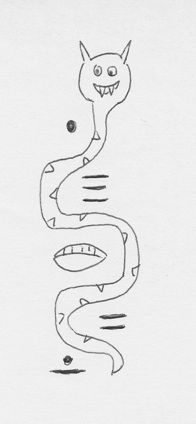
Figure 3. Isabel's birth date as a Mayan Serpent number. Amazing artwork by Amy and her son Brian, whose birth date is \(4.3.8.6.12.4\).
Pedro J. Freitas (Universidade de Lisboa) and Amy Shell-Gellasch (Beloit College), "When a Number System Loses Uniqueness: The Case of the Maya - The Mayan Number System," Convergence (June 2012), DOI:10.4169/loci003883




