- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Group Visualization with Group Explorer - Features: Visualization through Cayley Diagrams
Group Explorer's chief benefit is that it provides illustrations of objects and concepts from group theory that would otherwise be unavailable or cumbersome to create. The program automates the process of drawing and manipulating illustrations, such as Cayley diagrams and multiplication tables, to take the burden away from the user. But we haven't said yet what a Cayley diagram is. Before we continue, let us first introduce some important concepts on visualization in group theory.
There are several ways to visualize a group. The most significant and intuitive way was invented by the British mathematician Arthur Cayley and has been called the "Cayley diagram" after him. It has two major advantages over other visualization techniques. First, it clearly represents a group as a set of elements. This may not seem at first like anything significant, but we will see that other visualization techniques (e.g., multiplication tables or objects with symmetries) either do not directly represent the elements of the group or represent them redundantly. Second, by taking advantage of the group's generators, Cayley diagrams fully illustrate the interactions among the elements of the group while remaining minimally cluttered. As an added advantage, they are often quite pretty -- three examples appear in Figures 1 through 3. Each of these images was generated with Group Explorer.
Note: The notation aa in Figure 1 is more commonly written a2.
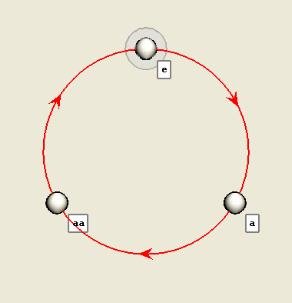
Figure 1. Cayley diagram of Z3
A Cayley diagram is a directed graph, or digraph. Each node of the graph represents one element of the group, and each type of directed edge represents a generator. In Figure 1 there are three nodes, each representing one of the three elements of the group; they are labeled e for the identity, a for the generator, and aa for the generator squared. And the red arrows show that multiplying by the generator a maps e to a, a to aa, and aa back to e. It is quite clear from the picture why this group is called "cyclic." Although Figure 1 is the only one on this page that explicitly names the elements of the group, each of Figures 1 through 3 highlights the identity element with a faint, round halo.
In the event that the group is not cyclic, there will be more than one generator, and thus more than one type of edge in the digraph. Figure 2 is the Cayley diagram of the smallest non-abelian group, S3, and its two generators are distinguished by color. The red arrows show the action of the order-3 generator, and the blue edges show the action of the order-2 generator. (The latter edges have no arrowheads because the generator is of order 2, and thus applies in both directions.)
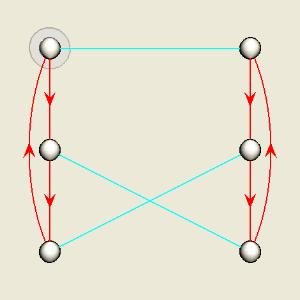
Figure 2. Cayley diagram of S3
A non-abelian group will contain a pair of generators that do not commute, and thus it will always be evident from the Cayley diagram whether or not a group is abelian. To see this in Figure 2, beginning with any element in the diagram, follow a red arrow and then a blue edge, and remember where you end up. Then repeat the experiment from your original starting place, but follow a blue arc first, then a red one. You will end at a different node.
Figure 3 shows a Cayley diagram for the symmetric group S4 and introduces one of the more basic modifications one can make to the plain vanilla Cayley diagram -- the nodes are colored to distinguish cosets of a three-element subgroup. (The subgroup itself is the set of three yellow nodes near the bottom containing the identity.) A more in-depth introduction to Cayley diagrams can be found in Fraleigh (2002), and a thorough treatment appears in Grossman & Magnus (1975), beginning in chapter six.
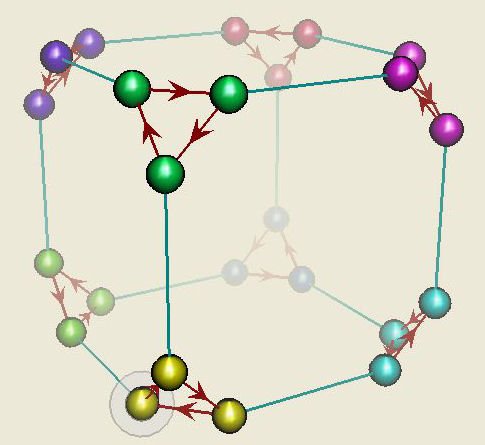
Figure 3. Cayley diagram of S4
Nathan Carter and Brad Emmons, "Group Visualization with [i]Group Explorer[/i] - Features: Visualization through Cayley Diagrams," Convergence (December 2005)




