- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Special Relativity and Conic Sections - Light Rays, Clocks, and Rulers: A Visual Primer
![]() Mathwright Microworld for this page
Mathwright Microworld for this page
|
|
PDF version of this page
|
Special relativity asserts (Einstein, 1921) that there exist frames of reference, called "inertial frames", with respect to which the laws of physics have the simplest possible expression and the equations all have the same form (principle of covariance). These inertial frames are, of course, a convenient fiction, giving only the infinitesimal approximation of the state of affairs in the presence of matter and energy. It is essentially the same as saying that a curved surface is "locally - in infinitesimal approximation" the same as a Euclidean space.
The inertial frames are what an observer uses to coordinatize the "world". And the world is space-time, or the world of "events". Inertial observers may associate numbers (coordinates) to the world of physical events, and once they do, they may derive relations among those numbers -- for example, that undisturbed bodies (such as the world lines of other inertial observers) describe straight lines, and that these straight lines have rulings determined by the ticking of the mover's clock.
Relativity asserts that all inertial coordinatizations of space-time are equivalent, in the sense that one cannot be distinguished from the other by any physical experiment. In particular, it is possible for inertial observers to come to agreement about their units of measure while they are stationary with respect to each other, and that, after this agreement is made, all will measure light to move at the same constant speed. This will be true whatever the subsequent state of relative motion of these observers.
This is astonishing, but it is what both experiment and Maxwell's Equations imply. All kinematic parameters may be expressed in terms of "light rays and clocks" from this viewpoint (Burke, 1985). The basic meaning of the principle of relativity is that there is no "privileged" viewpoint for the events in the physical world, but that there is a privileged class of inertial viewpoints, each equivalent one to the other, each indistinguishable from the others. They all describe the laws of physics in the same way.
To simplify the discussion, we suppress one of the dimensions of space-time and consider, instead of our four-dimensional space-time, a three-dimensional space-time. In this space-time there is a coordinatization by an inertial observer for which the velocity of light is 1. That is, light moves one unit distance in one unit of time. I shall call the coordinates of this space-time, as used by the inertial observer, ![]() .
.
To develop the physical interpretation of the focus-locus and focus-directrix properties of conic sections, I will work in this 2+1 dimensional space-time. As a preview, I mention that 2+1 space-time is a 3-dimensional vector space with a geometry very much like Euclidean geometry. That geometry is determined by the "hyperbolic metric", which I defined earlier.
Let us suppose that a "standard" observer is selected. Call that observer ![]() , and refer all spacetime events to the
, and refer all spacetime events to the ![]() coordinates that
coordinates that ![]() attaches to them. As I mentioned earlier, the name
attaches to them. As I mentioned earlier, the name ![]() will refer ambiguously to the observer himself and to the event of his first clock-tick. In this case the event
will refer ambiguously to the observer himself and to the event of his first clock-tick. In this case the event ![]() has standard coordinates
has standard coordinates ![]() . Now all spacetime events may be referred to these standard coordinates, for convenience of description. I call the event
. Now all spacetime events may be referred to these standard coordinates, for convenience of description. I call the event
|
|
the Origin event.
Next, suppose that there is another inertial observer. I assume that this observer has previously synchronized clocks and rulers with those of ![]() as described above. Call this observer
as described above. Call this observer ![]() . The new observer describes spacetime events with coordinates, say,
. The new observer describes spacetime events with coordinates, say, ![]() , and I assume that the event that
, and I assume that the event that ![]() describes as
describes as
|
|
is the same Origin event as that of ![]() . I will also refer to the event of the first clock tick of
. I will also refer to the event of the first clock tick of ![]() with
with ![]() coordinates
coordinates ![]() as
as ![]() .
.
We notice two things according to the covariance principle. If, in standard coordinates, the light cone at the origin is the set of events given by the equation
|
|
as measured by ![]() , then it coincides with the set of events given by the equation
, then it coincides with the set of events given by the equation
|
|
as measured by ![]() . That is,
. That is, ![]() and
and ![]() see the same light cone at the origin. But for an individual event on the light cone, they might assign different coordinates.
see the same light cone at the origin. But for an individual event on the light cone, they might assign different coordinates.
The same is true for the unit hyperboloid represented in standard coordinates as
|
|
While the event ![]() on that hyperboloid has standard coordinates
on that hyperboloid has standard coordinates ![]() , the event
, the event ![]() on that hyperboloid will in general have standard (
on that hyperboloid will in general have standard ( ![]() ) coordinates different from
) coordinates different from ![]() if
if ![]() is "in motion" with respect to
is "in motion" with respect to ![]() .
.
There is no absolute notion of simultaneity in Special Relativity, but each observer may define his own concept of simultaneity with a certain simple experiment with light and his clock that I will illustrate on this page. In particular, the events that observer ![]() considers to be "simultaneous" with his first clock-tick (the event
considers to be "simultaneous" with his first clock-tick (the event ![]() ) will be the plane tangent to the standard hyperboloid
) will be the plane tangent to the standard hyperboloid
|
|
at the point ![]() . This is the
. This is the ![]() plane for the observer
plane for the observer ![]() . We saw this plane in the Planes Intersecting Cones page. The intersection of this plane of events with the light cone at the origin was seen to be an ellipse in standard coordinates, with the Euclidean metric. That was the ellipse of the plane-slicing cone construction.
. We saw this plane in the Planes Intersecting Cones page. The intersection of this plane of events with the light cone at the origin was seen to be an ellipse in standard coordinates, with the Euclidean metric. That was the ellipse of the plane-slicing cone construction.
I emphasized standard ( ![]() ) coordinates because, from the point of view of
) coordinates because, from the point of view of ![]() , that set of events in the
, that set of events in the ![]() plane are simultaneous, and their intersection with the light cone at the origin forms a circle of radius 1. The points on this "ellipse" will not have constant t coordinates from the point of view of
plane are simultaneous, and their intersection with the light cone at the origin forms a circle of radius 1. The points on this "ellipse" will not have constant t coordinates from the point of view of ![]() , however. Now if
, however. Now if ![]() is actually in motion with respect to
is actually in motion with respect to ![]() then we have the following remarkable fact that will explain why an ellipse that is not a circle has a directrix. The plane of simultaneity
then we have the following remarkable fact that will explain why an ellipse that is not a circle has a directrix. The plane of simultaneity ![]() for
for ![]() intersects the plane of simultaneity t = 0 for
intersects the plane of simultaneity t = 0 for ![]() in a line!
in a line!
Let us illustrate with a picture. Suppose that our standard observer ![]() establishes the basis of coordinates
establishes the basis of coordinates ![]() for this 2+1 dimensional space-time. And suppose now that there is another inertial observer
for this 2+1 dimensional space-time. And suppose now that there is another inertial observer ![]() whose world line intersects the world line of
whose world line intersects the world line of ![]() at the origin, as above.
at the origin, as above.
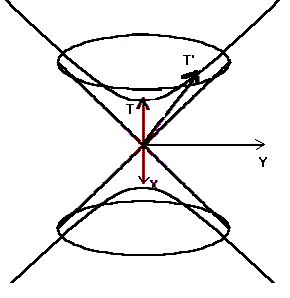 In particular, I assume that both
In particular, I assume that both ![]() and
and ![]() have clocks that tick time 0 for each at the origin event. What does this mean? The simplest way to picture it is to use the coordinates of
have clocks that tick time 0 for each at the origin event. What does this mean? The simplest way to picture it is to use the coordinates of ![]() to describe the event of the next tick of the clock of
to describe the event of the next tick of the clock of ![]() on the world-line of
on the world-line of ![]() . Certainly this event must occur in the future light cone of
. Certainly this event must occur in the future light cone of ![]() . But it cannot be just anywhere, for the following reason. The hyperbolic interval connecting the zero-th and first clock tick of
. But it cannot be just anywhere, for the following reason. The hyperbolic interval connecting the zero-th and first clock tick of ![]() along the world-line of
along the world-line of ![]() is obviously measured by
is obviously measured by ![]() to be -1. Therefore, it must be -1 in the coordinates of
to be -1. Therefore, it must be -1 in the coordinates of ![]() . This means that, in the coordinates of
. This means that, in the coordinates of ![]() , it lies on the hyperboloid
, it lies on the hyperboloid
![]()
as I observed above. The situation might be pictured as in the figure at the right.
From the picture, it is clear that the next clock tick of ![]() after the origin event must occur at a time that
after the origin event must occur at a time that ![]() will measure to be greater than or equal to 1. (This is the famous "time-contraction" -- the clock of
will measure to be greater than or equal to 1. (This is the famous "time-contraction" -- the clock of ![]() appears to be slower than that of
appears to be slower than that of ![]() .) It will be equal to 1 if and only if
.) It will be equal to 1 if and only if ![]() is not moving at all in the reference frame of
is not moving at all in the reference frame of ![]() , in which case the world-lines and the clocks of
, in which case the world-lines and the clocks of ![]() and
and ![]() coincide. The state of motion (with respect to
coincide. The state of motion (with respect to ![]() ) of observer
) of observer ![]() is almost determined by this picture. It is not entirely determined, because
is almost determined by this picture. It is not entirely determined, because ![]() still has some freedom in the choice of his spatial coordinates (vectors
still has some freedom in the choice of his spatial coordinates (vectors ![]() ). In order to make the analysis of the conics, I will have the standard observer choose the system of vectors
). In order to make the analysis of the conics, I will have the standard observer choose the system of vectors ![]() in a special way.
in a special way.
The line ![]() (the t-axis) is what I called the "world-line" of the observer
(the t-axis) is what I called the "world-line" of the observer ![]() . Points on the world-line are measured by the unit ticks of his clock. In this spacetime, a circular pulse of light emitted from the event
. Points on the world-line are measured by the unit ticks of his clock. In this spacetime, a circular pulse of light emitted from the event ![]() describes a cone (the light cone) of events along the wave-front of that pulse. It is described by the equation:
describes a cone (the light cone) of events along the wave-front of that pulse. It is described by the equation:
|
|
 A picture of the light cone (see the figure at the right) suggests that his world-line is "inside" the cone. It points "upward" in the
A picture of the light cone (see the figure at the right) suggests that his world-line is "inside" the cone. It points "upward" in the ![]() direction, towards the "future" for the observer.
direction, towards the "future" for the observer.
Now, while the ![]() axes are orthogonal in the Euclidean metric, the correct measure of distance in this 2+1 spacetime is given by the "hyperbolic" metric. Recall that, if
axes are orthogonal in the Euclidean metric, the correct measure of distance in this 2+1 spacetime is given by the "hyperbolic" metric. Recall that, if
![]() ,
,
then the inner product of ![]() , denoted
, denoted ![]() , is
, is
![]() .
.
All events in the observer's future are in the upper half of the light cone when we stipulate that the observer's "present" is the origin ![]() . In this sense, the observer can influence these future events from the "present" event by sending a signal (an inertial observer, or a ray of light) to them from the origin event, or from any event further along his world-line.
. In this sense, the observer can influence these future events from the "present" event by sending a signal (an inertial observer, or a ray of light) to them from the origin event, or from any event further along his world-line.
All events that are in the observer's past are in the bottom half of the light cone. An event is in the observer's past if a signal may come from that event to the origin, the present event ![]() .
.
In fact, it is possible for an observer to measure the interval between the origin event and any other event using clocks and light rays alone. An experiment on the dynamic version of this page will allow you to see that for yourself. It is worth our while to elaborate the last point, because it will give insight into our line of attack on conic sections. Assume that ![]() is an inertial observer whose clock has been synchronized with that of observer
is an inertial observer whose clock has been synchronized with that of observer ![]() as above, and for whom light travels with velocity 1. Suppose also that
as above, and for whom light travels with velocity 1. Suppose also that ![]() are events.
are events.
Imagine that at ![]() time
time ![]() , observer
, observer ![]() passes through event
passes through event ![]() . Now it is almost obvious that a unique ray of light may be emitted at some point on the world-line of
. Now it is almost obvious that a unique ray of light may be emitted at some point on the world-line of ![]() that will meet event
that will meet event ![]() . Let
. Let ![]() be the time (as measured by
be the time (as measured by ![]() ) of emission of that ray of light. And there is another unique ray if light that may be emitted from the event
) of emission of that ray of light. And there is another unique ray if light that may be emitted from the event ![]() that will arrive back on the world-line of
that will arrive back on the world-line of ![]() . We may consider this to be the reflection by a circular mirror situated in
. We may consider this to be the reflection by a circular mirror situated in ![]() . That reception event will occur at a time
. That reception event will occur at a time ![]() on the world line of
on the world line of ![]() . Obviously,
. Obviously, ![]() .
.
Now it takes light just as long to travel from the event at time ![]() on the world-line of
on the world-line of ![]() to
to ![]() as it takes to travel from
as it takes to travel from ![]() back to event at time
back to event at time ![]() on the world line of
on the world line of ![]() . Thus, in
. Thus, in ![]() coordinates, the time coordinate of event
coordinates, the time coordinate of event ![]() is midway between
is midway between ![]() and
and ![]() . It is
. It is
|
|
Also, since light travels with speed 1, the spatial coordinates of ![]() ,
, ![]() , satisfy
, satisfy
|
|
because that is how long it took light to reach ![]() .
.
Thus, when ![]() calculates the interval from
calculates the interval from ![]() to
to ![]() , he gets
, he gets
|
|
![]() can, in principle, make this measurement just with light (and a mirror) and his clock. In particular, if this product is 0, then
can, in principle, make this measurement just with light (and a mirror) and his clock. In particular, if this product is 0, then ![]() are connected by a light ray. If the product is positive, then
are connected by a light ray. If the product is positive, then ![]() must occur in the past of
must occur in the past of ![]() (before event
(before event ![]() on his world-line). And that would mean that
on his world-line). And that would mean that ![]() have a space-like interval.
have a space-like interval.
I put these ideas to use in the next section, A Thought Experiment, where I interpret the focus-locus definition of conic sections in terms of light cones.
James E. White, "Special Relativity and Conic Sections - Light Rays, Clocks, and Rulers: A Visual Primer," Convergence (October 2004)




