- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The SIR Model for Spread of Disease - Herd Immunity
Each strain of flu is a disease that confers future immunity on its sufferers. For such a disease, if almost everyone has had it, then those who have not had it are protected from getting it -- there are not enough susceptibles left in the population to allow an epidemic to get under way. This group protection is called herd immunity.
In Part 4 you experimented with the relative sizes of b and k, and you found that, if b is small enough relative to k, then no epidemic can develop. In the language of Part 5, if the contact number c = b/k is small enough, then there will be no epidemic. But another way to prevent an epidemic is to reduce the initial susceptible population artificially by inoculation.
The point of inoculation is to create herd immunity by stimulating in as many people as possible the antibodies that confer immunity -- but without actually giving those people the disease. Thus inoculation creates a direct path from the susceptible group to the recovered group without passing through the infected group (see the diagram below). And a large-scale inoculation program to head off an impending epidemic does this rapidly enough to lower the initial susceptible population to a safe level -- safe enough that if a trace level of infection enters the population, a few people may get sick, but no epidemic will develop.
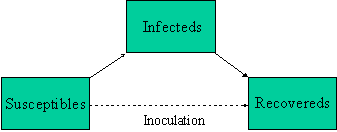
So, what fraction of the population must be inoculated to obtain herd immunity? Or, put another way, how small must s0 be to insure that an epidemic cannot get started? It depends on the contact number.
-
Explain why keeping an epidemic from getting started is the same as keeping di/dt negative from t = 0 on.
- Write the right-hand side of the infected-fraction differential equation

in factored form. Explain why one factor is always positive and why the sign of other factor depends on the size of s(t). -
Explain why s(t) is a decreasing function, and thus has its largest value at t = 0. It follows that, if di/dt is negative at time 0, then it stays negative.
- Show that
Explain why, if s0 is less than 1/c, then no epidemic can develop.

-
From 1912 to 1928, the contact number for measles in the U.S. was 12.8. If we assume that c is still 12.8 and that inoculation is 100% effective -- everyone inoculated obtains immunity from the disease -- what fraction of the population must be inoculated to prevent an epidemic?
-
Suppose the vaccine is only 95% effective. What fraction of the population would have to be inoculated to prevent a measles epidemic?
David Smith and Lang Moore, "The SIR Model for Spread of Disease - Herd Immunity," Convergence (December 2004)




