- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Transport Equation and Directional Derivatives - Solution of the Transport Equation
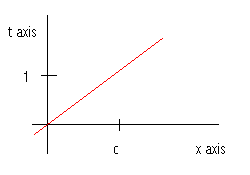 Using the gradient operator
Using the gradient operator

we may rewrite equation (1) as
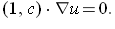
This equation says that the directional derivative in the (1, c) direction (in the
t, x-plane) is zero. So our solution u(x, t) must be constant in this direction. In the t, x-plane, the (1, c) direction is along lines parallel to x = ct, which are called the characteristics of equation (1).
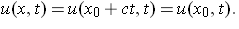
t, x-plane) is zero. So our solution u(x, t) must be constant in this direction. In the t, x-plane, the (1, c) direction is along lines parallel to x = ct, which are called the characteristics of equation (1).
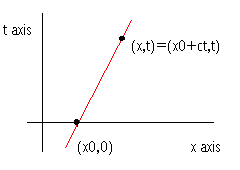
Now, fix a point on the x-axis, say (x0, 0). The line through this point parallel to x = ct
is given by x = x0 + ct. Since our solution is constant along this line, we must have
is given by x = x0 + ct. Since our solution is constant along this line, we must have
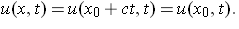
But from the initial data,
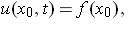
where f is known. So, for any (x, t),
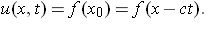
Joan Remski, "The Transport Equation and Directional Derivatives - Solution of the Transport Equation," Convergence (August 2004)




