- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Basic Ancient Model
The modern explanation described in Section 4 is an example of a geometric model for the motions of the planets—the apparent motions along the ecliptic are explained in terms of actual motions on geometric objects (circles). However, this explanation assumes a moving earth, which contradicts both intuition and “common sense.” Using just the evidence of their ordinary senses, it appeared to ancient people, as it does to us, that the earth is motionless while everything else in the sky—sun, moon, planets, and stars—moves in various ways. The ancient Greeks and Indians therefore sought a geometric model that accounted for the motions of the planets while leaving the earth at rest.
Such a model was probably first invented in the third century B.C.E. by the great Greek geometer Apollonius of Perga [13, p. 262]. (Apollonius is best known for his study of the conic sections—parabolas, ellipses, and hyperbolas—found in his book Conics.) In Apollonius’s model the planet moves uniformly around a circle called an epicycle, while the center of the epicycle moves uniformly around the earth on a larger circle called the deferent. Figure 6 illustrates this basic model; as can be seen, the model can generate retrograde motions quite well.
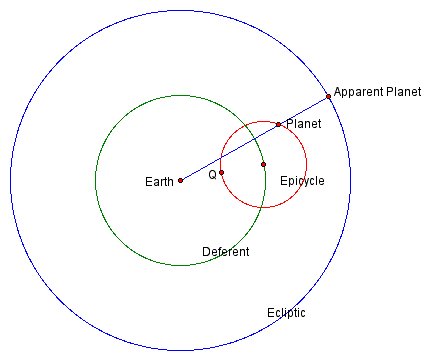
In circular motion, the time it takes an object to complete one full revolution around its circle is called its period. There are two periods in the basic ancient model: the period of the epicycle center as it revolves around the deferent, and the period of the planet as it revolves round the epicycle. The first period represents the time it takes the planet, on average, to return to the same point of the ecliptic; this is called the sidereal period. The latter period could be taken to be the time between successive returns of the planet to the point Q in the diagram; as such it represents the time between the middles of successive retrograde motions. This period is called the synodic period.
The basic model has three parameters. These are: r/R, where r is the radius of the epicycle and R is the radius of the deferent; the sidereal period T; and the synodic period S. In Figure 6, dragging the points labeled r/R, T, and S will change these parameters. The reader should observe how varying these quantities changes the planet’s motion, in particular the spacing, duration, or size of the retrograde arcs.
Like the basic modern model, this ancient model gives only a crude approximation to the motions of the planets. For example, the model implies that a planet’s retrograde arcs are all evenly spaced on the ecliptic, and are all of the same length. Because of the careful and systematic observations of the Babylonians, ancient astronomers knew this not to be the case: a planet’s retrograde arcs vary in both spacing and length. To account for irregularities like this, the actual models used by the Greeks and Indians incorporated other geometric devices into the underlying blueprint of the basic model. Nonetheless, we will use the basic model to derive an approximate quantitative description of the motions of the planets. In this way we will gain some insight into the mathematical techniques of early planetary theory and in particular its use of trigonometry.
To convert the basic model into a quantitative description of a planet’s motion, specific values for the parameters must be derived. We carry out this task in Sections 6 and 7.
Sandra M. Caravella (New Jersey City University), "Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Basic Ancient Model," Convergence (August 2010), DOI:10.4169/loci003120




