- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Bloom's Taxonomy in Developing Assessment Items - Course Content
The catalog description of the precalculus course we teach at Georgia State lists the content areas: trigonometric functions, identities, inverses, and equations; vectors; polar coordinates; conic sections. The current textbook is Barnett, Ziegler, and Byleen (2001).
The content standards (CS) developed by our department and used as guidelines for teaching the course are organized into eight groups:
- CS1. Quantitative Reasoning
- CS2. Abstract and Algebraic Functions
- CS3. Defining the Trigonometric Functions
- CS4. Use of the Trigonometric Functions
- CS5. Mathematical Proofs
- CS6. Analytic Geometry
- CS7. Vectors
- CS8. Applications
Each CS contains detailed requirements regarding the acquisition of knowledge and skills that students are expected to meet upon the completion of the course. These standards move beyond simple computations to understanding and relating concepts. When possible, problems are based on the use of multiple representations. For example, consider the problem of conversion between rectangular and polar coordinates for a point P. Instead of using only algebraic formulas, an item may encourage or even require students to also use a diagram with rectangular and polar coordinate systems overlaid, as shown in Figure 1. After plotting the point in one system, the coordinates can be read from the other.
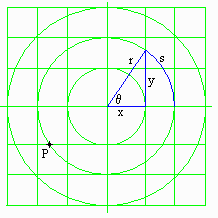
Figure 1: Multiple representations
The concepts and problems of a precalculus course can be very different from those of the prerequisite algebra courses. In preceding courses, students may have seen computation and algebraic manipulations emphasized. By contrast, this course should be highly visual. Our materials emphasize the geometry of triangles and circles. Properties of functions such as increasing, slope, asymptotes, foci, vertex, directrix, periodicity, and amplitude are illustrated through their graphs. In addition, many concepts are understood, explored, and manipulated using diagrams. This includes diagrams for winding functions, transformations of graphs, transformations of coordinate systems, vector addition, and vector resolution.
In the next section we describe the course design and organization of the WebCT-based Precalculus as taught by four faculty in our department. We refer to these classes as the "experimental sections."
Draga Vidakovic, Jean Bevis, and Margo Alexander, "Bloom's Taxonomy in Developing Assessment Items - Course Content," Convergence (December 2004)




