- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Raindrops - Summary
- Why is it important to consider air resistance when modeling raindrops as falling objects?
- What important feature did you find in both resistance models that was lacking in the no-resistance model? How did the slope fields reveal this feature? How does it appear symbolically in the differential equations?
- Explain in your own words how Euler's Method generates a solution of an initial value problem. In particular, explain how Euler's Method uses the same information that is used to generate a slope field.
- Explain why
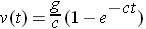
is an exact solution of the drizzle drop problem. How does this formula reveal the terminal velocity you know already? If you guessed the form of the solution on Page 3, compare this symbolic form with your guess. Are the two proposed solutions the same? If not, describe how they differ.
Final comments
- You may wonder why we didn't study a model for raindrops between very large and very small drops. For most of the size range, no one knows an accurate model as simple as those studied here. However, the evidence at both ends of the range suggests that one might as well assume that all raindrops fall at terminal velocity most of the time -- a velocity very much dependent on the size of the drops.
- In Step 4 above, you confirmed an exact formula for the solution of the falling body problem with linear resistance. You may have already encountered this formula in a calculus course. There is also an exact formula for the solution of the quadratic resistance problem (thunderstorm drops), but it is much more complicated and not likely to appear early in a calculus course. Observe that the information we get from Euler's Method is the same in both cases -- and that it doesn't depend on whether there is a formula for the solution, or on whether we know the formula if there is one.
David A. Smith and Lawrence C. Moore, "Raindrops - Summary," Convergence (December 2004)




