- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Three Party Elections: Interactive Examples - Shifting Groups of Voters
Instead of adding voters one at a time to the six regions of the representation triangle, we can make many interesting observations by adding voters as a group, or shifting voters' preferences in specific ways. We can think of this as adding two six-dimensional vectors:
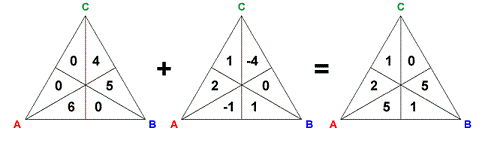
Adding a negative numbers reduces the number of voters with that preference, whereas adding a positive numbers increases the number of voters with that preference. Naturally, adding or subtracting voters in this way can change the winner of the election. For the original triangle in the example above, the Condorcet winner was B, but after applying the changes the Condorcet winner is now A.
The triangle below is represented by the vector (u, v, w, x, y, z).
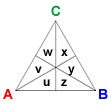
We want to think about ways that we can add or shift voters that are not just random. For example, if a vector represents a "tied" vote in some way, then adding this vector to a profile vector should not change the outcome corresponding to the profile. In addition, we are interested in a basis for the vector space of all voter profiles, since this will give us a way to decompose profiles and understand how the various methods for selecting a winner apply.
In this section we present a basis for this vector space from [1]. Each vector is given as a representation triangle, and the effects on the positional and Condorcet methods of adding this vector are discussed.
Kernel Vector
The kernel vector is K = (1, 1, 1, 1, 1, 1). Adding K to a profile adds one voter to each of the six preference orders.
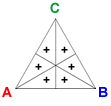
- Positional method: Each candidate's total is increased by 2 + 2s, so the result of the positional method is unchanged.
- Condorcet method: In each of the pairwise elections, each candidate has 3 additional votes, so the results of these elections are unchanged.
Condorcet Vector
The Condorcet vector is C = (1, −1, 1, −1, 1, −1). Adding C to a profile adds a voter to preferences A > B > C, B > C > A, and C > A > B, and deducts a voter from the reverse preferences C > B > A, A > C > B, and B > A > C.
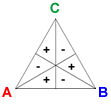
- Positional method: Each candidate's total is unchanged, since she has the same number of first-place and second-place votes as before.
- Condorcet method: In each of the pairwise elections, one candidate receives one additional vote and the other receives one fewer vote. Preference is given to A over B, B over C, and C over A. If enough Condorcet terms are added, a Condorcet cycle will result.
Reversal Vectors
The vectors Reversal A, Reversal B,and Reversal C are defined by RA = (1, 1, −2, 1, 1, −2), RB = (−2, 1, 1, −2, 1, 1), and RC = (1, −2, 1, 1, −2, 1).
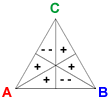
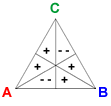
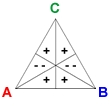
The reversal vector for a candidate corresponds to splitting two second-place votes for the candidate into a first and third-place vote. For example, adding RA to a profile deducts 2 votes each from the two preferences where A is second-ranked, and adds one vote each to the remaining four preference orders.
- Positional method: If RA is added, A's total is increased by 2 − 4s, and B's and C's totals are increased by −1 + 2s.
- if s < 0.5, then this increases A's total and reduces B's and C's totals equally.
- if s = 0.5, then this leaves all three totals unchanged.
- if s > 0.5, then this decreases A's total and increases B's and C's totals equally.
- Condorcet method: None of the reversal terms affect the outcomes of the pairwise elections. Each candidate's total in pairwise elections is unchanged.
Note that RC = −(RA + RB). So we need only include RA and RB in our basis.
Basic Vectors
The vectors Basic A, Basic B, and Basic C are defined by BA = (1, 1, 0, −1, −1, 0), BB = (0, −1, −1, 0, 1, 1), and BC = (−1, 0, 1, 1, 0, −1).
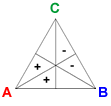
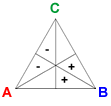
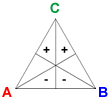
Addition of a candidate's basic vector to a profile shifts one vote each from the two preference orders where the candidate is lowest-ranked to those in which she is highest ranked.
- Positional method: In every positional method, addition of a candidate's basic vector increases her total by 2 while reducing the totals of the other candidates by 1. Each candidate's number of second-place votes remains unchanged. Adding enough of a candidate's basic vector will make her the winner of all positional methods.
- Condorcet method: Addition of a candidate's basic vector does not affect the pairwise election that she is not involved in. However, it does give the candidate a 2-vote swing in both of her pairwise elections. If enough basic vectors are added for a candidate, she will be the Condorcet winner.
Note that BC = −(BA + BB). So we need only include BA and BB in our basis.
The Basis
The set {K, C, RA, RB, BA, BB} forms a basis for the six-dimensional vector space of voter profiles. Note that with the exception of the kernel vector, the entries of all of these vectors sum to zero. Hence we can think of these vectors as representing a shift in voter preference that does not change the total number of votes.
In the interactive mathlet below, experiment with creating profiles by adding or subtracting these basis vectors. Notice that repeatedly adding K or any of the reversal vectors does not change the Condorcet winner. Notice that repeatedly adding K or C does not change the positional outcome. Finally note that repeatedly adding a basic vector will eventually make that candidate the winner of both methods.
Constructing Examples
Many interesting examples come from voter profiles where one candidate wins using one method, but loses using a different method. How can we use these vector ideas to construct such examples?
Example
Suppose that you want to construct an example in which A wins the positional method with s = 0.7, but B is the Condorcet winner.
In general, there are two ways to make A win the positional method with s = 0.7: add copies of Basic A or subtract copies of Reversal A (since s > 0.5). Since copies of Basic A would also make A the Condorcet winner, we will choose to subtract Reversal A. Follow these steps to construct the example.
- Reset the mathlet above.
- Drag the positional method slider so that s is approximately 0.7.
- Right-click the Reversal A triangle three times. Remember that left-clicking a vector adds it to the profile, and right-clicking subtracts it. Notice that all of the pairwise elections are tied 0 to 0.
- In order to make B the Condorcet winner, we should add copies of Basic B, but if we add too many, we will make B the positional winner also, which is not what we want. Adding a single copy of Basic B is enough, but two copies would be too many.
- If we want a profile where all the preferences have a non-negative number of voters, we can simply add four copies of the Kernel vector. Notice that adding and subtracting the Kernel vector doesn't change the outcomes of any of the elections.
By understanding the effect that each vector has on each election method, we can easily construct many examples of "paradoxical" elections. We can also use linear algebra techniques to decompose a given profile relative to the six basis vectors. Profiles with Condorcet cycles will have a large C component. Profiles with candidate B winning all of the election methods will have a large BB component, and so on.
James E. Hamblin, "Three Party Elections: Interactive Examples - Shifting Groups of Voters," Convergence (July 2006)




